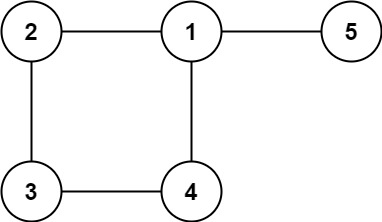
目标
给你两个正整数 xCorner 和 yCorner 和一个二维整数数组 circles ,其中 circles[i] = [xi, yi, ri] 表示一个圆心在 (xi, yi) 半径为 ri 的圆。
坐标平面内有一个左下角在原点,右上角在 (xCorner, yCorner) 的矩形。你需要判断是否存在一条从左下角到右上角的路径满足:路径 完全 在矩形内部,不会 触碰或者经过 任何 圆的内部和边界,同时 只 在起点和终点接触到矩形。
如果存在这样的路径,请你返回 true ,否则返回 false 。
示例 1:
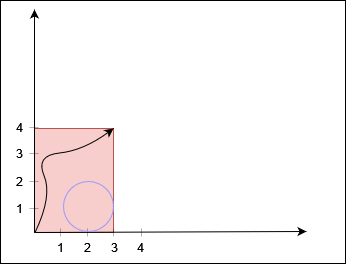
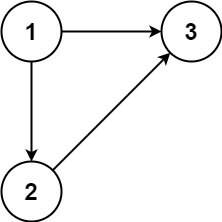
输入:X = 3, Y = 4, circles = [[2,1,1]]
输出:true
解释:
黑色曲线表示一条从 (0, 0) 到 (3, 4) 的路径。示例 2:
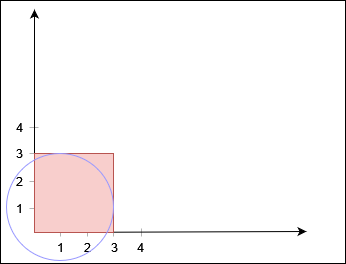
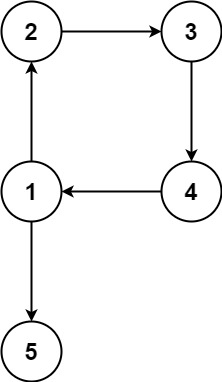
输入:X = 3, Y = 3, circles = [[1,1,2]]
输出:false
解释:
不存在从 (0, 0) 到 (3, 3) 的路径。示例 3:
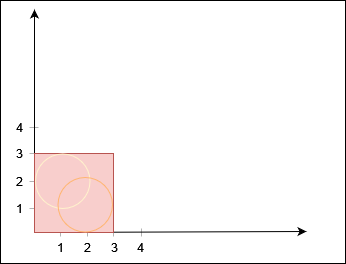
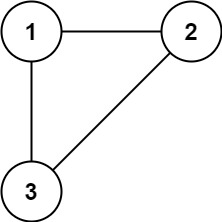
输入:X = 3, Y = 3, circles = [[2,1,1],[1,2,1]]
输出:false
解释:
不存在从 (0, 0) 到 (3, 3) 的路径。示例 4:
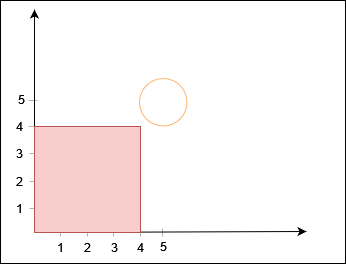
输入:X = 4, Y = 4, circles = [[5,5,1]]
输出:true
解释:说明:
- 3 <= xCorner, yCorner <= 10^9
- 1 <= circles.length <= 1000
- circles[i].length == 3
- 1 <= xi, yi, ri <= 10^9
思路
有一个以原点为左下顶点, [xCorner, yCorner] 为右上顶点的矩形,还有一些圆 circles,circles[i, j, r] 表示圆的圆心在 (i, j) 半径为 r。问是否存在一条从原点到 [xCorner, yCorner] 的路径,满足路径在矩形内部(不与矩形边界重合),且不触碰或经过任何园的内部与边界。
评论说这是史上分数最高的题目,周赛全球也没几个人做出来,直接放弃了。
代码