目标
你正在把积木堆成金字塔。每个块都有一个颜色,用一个字母表示。每一行的块比它下面的行 少一个块 ,并且居中。
为了使金字塔美观,只有特定的 三角形图案 是允许的。一个三角形的图案由 两个块 和叠在上面的 单个块 组成。模式是以三个字母字符串的列表形式 allowed 给出的,其中模式的前两个字符分别表示左右底部块,第三个字符表示顶部块。
- 例如,"ABC" 表示一个三角形图案,其中一个 “C” 块堆叠在一个 'A' 块(左)和一个 'B' 块(右)之上。请注意,这与 "BAC" 不同,"B" 在左下角,"A" 在右下角。
你从作为单个字符串给出的底部的一排积木 bottom 开始,必须 将其作为金字塔的底部。
在给定 bottom 和 allowed 的情况下,如果你能一直构建到金字塔顶部,使金字塔中的 每个三角形图案 都是在 allowed 中的,则返回 true ,否则返回 false 。
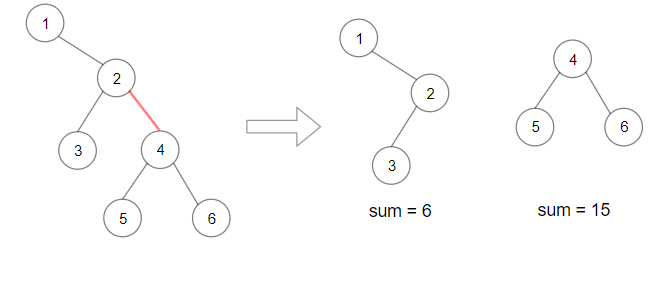
示例 1:
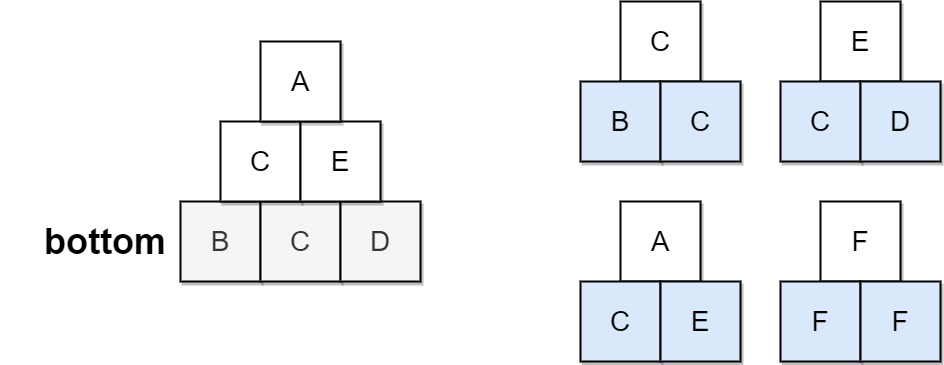
输入:bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"]
输出:true
解释:允许的三角形图案显示在右边。
从最底层(第 3 层)开始,我们可以在第 2 层构建“CE”,然后在第 1 层构建“E”。
金字塔中有三种三角形图案,分别是 “BCC”、“CDE” 和 “CEA”。都是允许的。
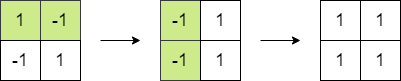
示例 2:
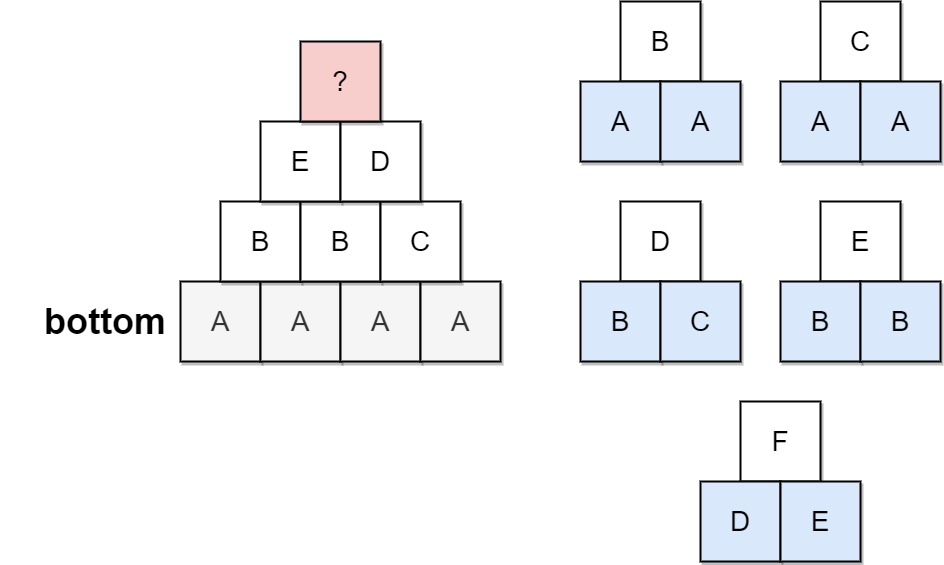
输入:bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"]
输出:false
解释:允许的三角形图案显示在右边。
从最底层(即第 4 层)开始,创造第 3 层有多种方法,但如果尝试所有可能性,你便会在创造第 1 层前陷入困境。
说明:
- 2 <= bottom.length <= 6
- 0 <= allowed.length <= 216
- allowed[i].length == 3
- 所有输入字符串中的字母来自集合 {'A', 'B', 'C', 'D', 'E', 'F'}。
- allowed 中所有值都是 唯一的
思路
有一排积木 bottom,将其作为金字塔的底部,又有一个模式列表 allowed,每个模式是一个长度为 3 的字符串 pattern,表示 pattern[2] 堆叠在左侧的 pattern[0] 和右侧的 pattern[1] 之上。判断能否使用给定的模式堆成一个金字塔。
使用哈希表保存 pattern 下面两个与上面一个的对应关系,dfs 暴力枚举所有可能,分为两个维度,枚举当前层所有可能的排列,生成下一层所有可能的排列;枚举特定的上一层排列生成对应可能的排列。
代码
/**
* @date 2025-12-29 9:23
*/
public class PyramidTransition756 {
public boolean pyramidTransition(String bottom, List<String> allowed) {
int n = bottom.length();
Map<String, Set<Character>> map = new HashMap<>();
for (String s : allowed) {
String key = s.substring(0, 2);
map.putIfAbsent(key, new HashSet<>());
map.get(key).add(s.charAt(2));
}
Set<String> candidates = new HashSet<>();
candidates.add(bottom);
Set<String> top = dfs(1, n, map, candidates);
return top.size() > 0;
}
public Set<String> dfs(int l, int n, Map<String, Set<Character>> map, Set<String> candidates) {
if (l == n) {
return candidates;
}
Set<String> next = new HashSet<>();
for (String prev : candidates) {
Set<String> tmp = new HashSet<>();
dfs(1, prev, "", map, tmp);
next.addAll(tmp);
}
return dfs(l + 1, n, map, next);
}
public void dfs(int index, String prev, String row, Map<String, Set<Character>> map, Set<String> set) {
if (index == prev.length()) {
if (!"".equals(row)) {
set.add(row);
}
return;
}
String key = prev.charAt(index - 1) + String.valueOf(prev.charAt(index));
Set<Character> characters = map.get(key);
if (characters != null) {
for (Character c : characters) {
dfs(index + 1, prev, row + c, map, set);
}
}
}
}
性能