目标
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
- horizontalCut 的大小为 m - 1 ,其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。
- verticalCut 的大小为 n - 1 ,其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
- 沿着水平线 i 切开蛋糕,开销为 horizontalCut[i] 。
- 沿着垂直线 j 切开蛋糕,开销为 verticalCut[j] 。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
示例 1:
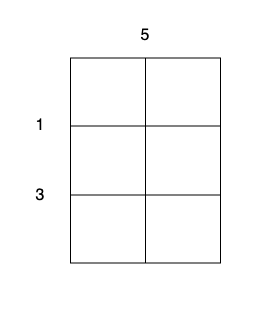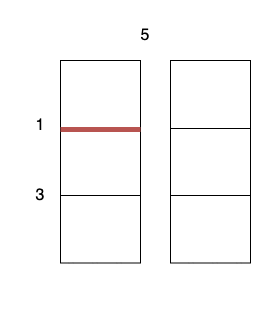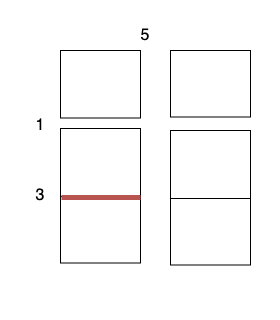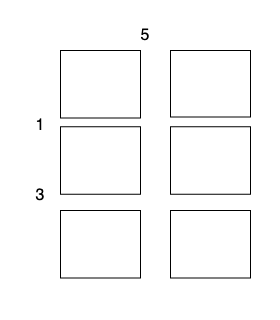
输入:m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]
输出:13
解释:
沿着垂直线 0 切开蛋糕,开销为 5 。
沿着水平线 0 切开 3 x 1 的蛋糕块,开销为 1 。
沿着水平线 0 切开 3 x 1 的蛋糕块,开销为 1 。
沿着水平线 1 切开 2 x 1 的蛋糕块,开销为 3 。
沿着水平线 1 切开 2 x 1 的蛋糕块,开销为 3 。
总开销为 5 + 1 + 1 + 3 + 3 = 13 。
示例 2:
输入:m = 2, n = 2, horizontalCut = [7], verticalCut = [4]
输出:15
解释:
沿着水平线 0 切开蛋糕,开销为 7 。
沿着垂直线 0 切开 1 x 2 的蛋糕块,开销为 4 。
沿着垂直线 0 切开 1 x 2 的蛋糕块,开销为 4 。
总开销为 7 + 4 + 4 = 15 。
说明:
- 1 <= m, n <= 20
- horizontalCut.length == m - 1
- verticalCut.length == n - 1
- 1 <= horizontalCut[i], verticalCut[i] <= 10^3
思路
有一块 m x n 的蛋糕,horizontalCut[i] 表示水平切第 i 行的开销,verticalCut[i] 表示垂直切第 i 列的开销。求将蛋糕切成 1 x 1 小块的最小代价。
需要注意每次切的蛋糕必须是整块的,并不能将几块蛋糕排到一起切。
我们应该先沿着代价最大的位置切吗?比如大小为 2 x 100 的蛋糕,水平切的代价为 99,垂直切每一列的代价为 100。先切每一列代价为 99 * 100,然后对切开的 100 块水平切 100 次,代价为 100 * 99,总代价为 2 * 99 * 100。如果先水平切一次,代价为 99。然后需要垂直切 2 * 99 次,代价为 2 * 99 * 100,总代价为 99 + 2 * 99 * 100。这种贪心策略应该是可行的,因为每切一次块数会增加,现在不切代价大的,后面再切的时候代价会增加。
选择沿某一水平或垂直线切割时,需要记录水平 和 垂直方向蛋糕块的数量,用来计算代价。每切一次,横向与纵向的蛋糕块就会增加一个。
刚开始不确定能否使用贪心策略,考虑如何表示哪些切过了,哪些没切,卡了很久。关键点是如何将问题抽象建模,使用分治思想,不要面向过程。每切一次之后,问题转化为切剩余蛋糕的子问题。我们可以使用记忆化搜索解空间,求出最小值。
代码
/**
* @date 2024-12-25 10:41
*/
public class MinimumCost3218 {
public int minimumCost_v1(int m, int n, int[] horizontalCut, int[] verticalCut) {
int horizontalCutPart = 1;
int verticalCutPart = 1;
Arrays.sort(horizontalCut);
Arrays.sort(verticalCut);
int h = horizontalCut.length - 1;
int v = verticalCut.length - 1;
int res = 0;
while (h >= 0 || v >= 0) {
if (h < 0){
res += horizontalCutPart * verticalCut[v];
v--;
continue;
}
if (v < 0){
res += verticalCutPart * horizontalCut[h];
h--;
continue;
}
if (horizontalCut[h] > verticalCut[v]) {
res += verticalCutPart * horizontalCut[h];
horizontalCutPart++;
h--;
} else if (horizontalCut[h] <= verticalCut[v]) {
res += horizontalCutPart * verticalCut[v];
verticalCutPart++;
v--;
}
}
return res;
}
int[] rowCost;
int[] colCost;
int[][][][] mem;
public int minimumCost(int m, int n, int[] horizontalCut, int[] verticalCut) {
this.rowCost = horizontalCut;
this.colCost = verticalCut;
mem = new int[m + 1][m + 1][n + 1][n + 1];
// rowStart rowEnd colStart colEnd 表示蛋糕的边界
// 0 1 2 3 4 5 ... n
// 0 ———————————————————
// | | | | | |
// 1 ———————————————————
// | | | | | |
// 2 ———————————————————
// | | | | | |
// 3 ———————————————————
// | | | | | |
// 4 ———————————————————
// | | | | | |
// 5 ———————————————————
// ...
// m
return dfs(0, m, 0, n);
}
public int dfs(int rowStart, int rowEnd, int colStart, int colEnd) {
if (rowEnd - rowStart == 1 && colEnd - colStart == 1) {
return 0;
}
int res = Integer.MAX_VALUE;
for (int i = rowStart + 1; i < rowEnd; i++) {
if (mem[rowStart][i][colStart][colEnd] == 0) {
mem[rowStart][i][colStart][colEnd] = dfs(rowStart, i, colStart, colEnd);
}
if (mem[i][rowEnd][colStart][colEnd] == 0) {
mem[i][rowEnd][colStart][colEnd] = dfs(i, rowEnd, colStart, colEnd);
}
res = Math.min(res, rowCost[i - 1] + mem[rowStart][i][colStart][colEnd] + mem[i][rowEnd][colStart][colEnd]);
}
for (int i = colStart + 1; i < colEnd; i++) {
if (mem[rowStart][rowEnd][colStart][i] == 0) {
mem[rowStart][rowEnd][colStart][i] = dfs(rowStart, rowEnd, colStart, i);
}
if (mem[rowStart][rowEnd][i][colEnd] == 0) {
mem[rowStart][rowEnd][i][colEnd] = dfs(rowStart, rowEnd, i, colEnd);
}
res = Math.min(res, colCost[i - 1] + mem[rowStart][rowEnd][colStart][i] + mem[rowStart][rowEnd][i][colEnd]);
}
return res;
}
}
性能