目标
给你一个正整数 n ,表示最初有一个 n x n 、下标从 0 开始的整数矩阵 mat ,矩阵中填满了 0 。
另给你一个二维整数数组 queries 。针对每个查询 queries[i] = [row1i, col1i, row2i, col2i] ,请你执行下述操作:
- 找出 左上角 为 (row1i, col1i) 且 右下角 为 (row2i, col2i) 的子矩阵,将子矩阵中的 每个元素 加 1 。也就是给所有满足 row1i <= x <= row2i 和 col1i <= y <= col2i 的 mat[x][y] 加 1 。
返回执行完所有操作后得到的矩阵 mat 。
示例 1:
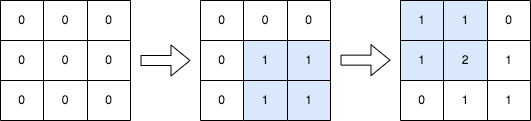
输入:n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出:[[1,1,0],[1,2,1],[0,1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作:将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。
- 第二个操作:将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。 示例 2:

输入:n = 2, queries = [[0,0,1,1]]
输出:[[1,1],[1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵。
- 第一个操作:将矩阵中的每个元素加 1 。说明:
- 1 <= n <= 500
- 1 <= queries.length <= 10^4
- 0 <= row1i <= row2i < n
- 0 <= col1i <= col2i < n
思路
有一个元素值为 0 的 n x n 矩阵 mat 和一系列由左上 (r1, c1) 右下 (r2, c2) 两个顶点表示的子矩阵,依次操作这些子矩阵,使其中的所有元素值加 1,返回最终得到的矩阵。
考察二维差分数组 以及 二维前缀和,这里直接当作多个一维差分处理了。
代码
/**
* @date 2025-11-14 8:59
*/
public class RangeAddQueries2536 {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] diff = new int[n][n + 1];
for (int[] query : queries) {
int row1 = query[0];
int row2 = query[2];
int col1 = query[1];
int col2 = query[3];
for (int j = row1; j <= row2; j++) {
diff[j][col1]++;
diff[j][col2 + 1]--;
}
}
int[][] res = new int[n][n];
for (int i = 0; i < n; i++) {
int[] row = diff[i];
res[i][0] = row[0];
for (int j = 1; j < n; j++) {
res[i][j] = res[i][j - 1] + row[j];
}
}
return res;
}
}
性能
