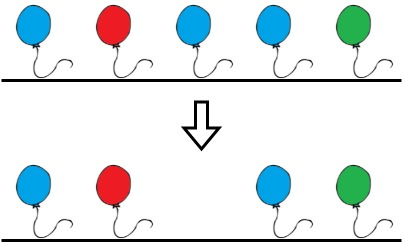
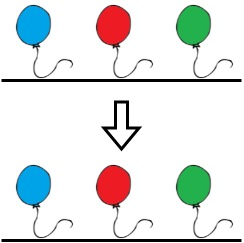
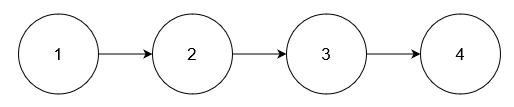
目标
给你一个整数 c,表示 c 个电站,每个电站有一个唯一标识符 id,从 1 到 c 编号。
这些电站通过 n 条 双向 电缆互相连接,表示为一个二维数组 connections,其中每个元素 connections[i] = [ui, vi] 表示电站 ui 和电站 vi 之间的连接。直接或间接连接的电站组成了一个 电网 。
最初,所有 电站均处于在线(正常运行)状态。
另给你一个二维数组 queries,其中每个查询属于以下 两种类型之一 :
- [1, x]:请求对电站 x 进行维护检查。如果电站 x 在线,则它自行解决检查。如果电站 x 已离线,则检查由与 x 同一 电网 中 编号最小 的在线电站解决。如果该电网中 不存在 任何 在线 电站,则返回 -1。
- [2, x]:电站 x 离线(即变为非运行状态)。
返回一个整数数组,表示按照查询中出现的顺序,所有类型为 [1, x] 的查询结果。
注意:电网的结构是固定的;离线(非运行)的节点仍然属于其所在的电网,且离线操作不会改变电网的连接性。
示例 1:
输入: c = 5, connections = [[1,2],[2,3],[3,4],[4,5]], queries = [[1,3],[2,1],[1,1],[2,2],[1,2]]
输出: [3,2,3]
解释:
最初,所有电站 {1, 2, 3, 4, 5} 都在线,并组成一个电网。
查询 [1,3]:电站 3 在线,因此维护检查由电站 3 自行解决。
查询 [2,1]:电站 1 离线。剩余在线电站为 {2, 3, 4, 5}。
查询 [1,1]:电站 1 离线,因此检查由电网中编号最小的在线电站解决,即电站 2。
查询 [2,2]:电站 2 离线。剩余在线电站为 {3, 4, 5}。
查询 [1,2]:电站 2 离线,因此检查由电网中编号最小的在线电站解决,即电站 3。
示例 2:
输入: c = 3, connections = [], queries = [[1,1],[2,1],[1,1]]
输出: [1,-1]
解释:
没有连接,因此每个电站是一个独立的电网。
查询 [1,1]:电站 1 在线,且属于其独立电网,因此维护检查由电站 1 自行解决。
查询 [2,1]:电站 1 离线。
查询 [1,1]:电站 1 离线,且其电网中没有其他电站,因此结果为 -1。
说明:
- 1 <= c <= 10^5
- 0 <= n == connections.length <= min(10^5, c * (c - 1) / 2)
- connections[i].length == 2
- 1 <= ui, vi <= c
- ui != vi
- 1 <= queries.length <= 2 * 10^5
- queries[i].length == 2
- queries[i][0] 为 1 或 2。
- 1 <= queries[i][1] <= c
思路
有 c 个电站,编号为 1 ~ c,connections[i] = [ui, vi] 表示电站 ui 与 vi 相连,所有连通的电站组成了一个电网。查询 queries[i] = [operation, x],如果 operation 为 2 表示将电站 x 离线,如果 operation 为 1 并且 x 在线,返回 x,否则返回 x 所在电网中在线电站的最小编号,如果没有在线电站返回 -1。
使用 有序集合 数组 维护不同电网的在线电站。如果离线就将其从有序集合中删掉 O(logn),否则先判断集合是否为空,如果集合为空返回 -1,再判断电站是否在集合中 O(logn),如果在则直接返回查询电站编号,否则取集合最小的编号。
代码
/**
* @date 2025-11-06 9:03
*/
public class ProcessQueries3607 {
private class UnionFind {
private int[] fa;
public UnionFind() {
}
public UnionFind(int n) {
this.fa = new int[n];
Arrays.setAll(this.fa, i -> i);
}
public int find(int x) {
if (fa[x] != x) {
fa[x] = find(fa[x]);
}
return fa[x];
}
public void merge(int x, int y) {
int a = find(x);
int b = find(y);
if (a != b) {
fa[b] = a;
}
}
}
public int[] processQueries(int c, int[][] connections, int[][] queries) {
UnionFind uf = new UnionFind(c + 1);
for (int[] connection : connections) {
uf.merge(connection[0], connection[1]);
}
TreeSet<Integer>[] set = new TreeSet[c + 1];
Arrays.setAll(set, i -> new TreeSet<>());
for (int i = 1; i <= c; i++) {
set[uf.find(i)].add(i);
}
List<Integer> list = new ArrayList<>();
boolean[] off = new boolean[c + 1];
for (int[] query : queries) {
int operation = query[0];
int node = query[1];
int network = uf.find(node);
if (operation == 1) {
if (set[network].size() > 0) {
if (off[node]) {
list.add(set[network].first());
} else {
list.add(node);
}
} else {
list.add(-1);
}
} else {
off[node] = true;
set[network].remove(node);
}
}
return list.stream().mapToInt(i -> i).toArray();
}
}
性能