目标
给你一个长度为 n 的二维整数数组 items 和一个整数 k 。
items[i] = [profiti, categoryi],其中 profiti 和 categoryi 分别表示第 i 个项目的利润和类别。
现定义 items 的 子序列 的 优雅度 可以用 total_profit + distinct_categories^2 计算,其中 total_profit 是子序列中所有项目的利润总和,distinct_categories 是所选子序列所含的所有类别中不同类别的数量。
你的任务是从 items 所有长度为 k 的子序列中,找出 最大优雅度 。
用整数形式表示并返回 items 中所有长度恰好为 k 的子序列的最大优雅度。
注意:数组的子序列是经由原数组删除一些元素(可能不删除)而产生的新数组,且删除不改变其余元素相对顺序。
示例 1:
输入:items = [[3,2],[5,1],[10,1]], k = 2
输出:17
解释:
在这个例子中,我们需要选出长度为 2 的子序列。
其中一种方案是 items[0] = [3,2] 和 items[2] = [10,1] 。
子序列的总利润为 3 + 10 = 13 ,子序列包含 2 种不同类别 [2,1] 。
因此,优雅度为 13 + 22 = 17 ,可以证明 17 是可以获得的最大优雅度。
示例 2:
输入:items = [[3,1],[3,1],[2,2],[5,3]], k = 3
输出:19
解释:
在这个例子中,我们需要选出长度为 3 的子序列。
其中一种方案是 items[0] = [3,1] ,items[2] = [2,2] 和 items[3] = [5,3] 。
子序列的总利润为 3 + 2 + 5 = 10 ,子序列包含 3 种不同类别 [1, 2, 3] 。
因此,优雅度为 10 + 32 = 19 ,可以证明 19 是可以获得的最大优雅度。
示例 3:
输入:items = [[1,1],[2,1],[3,1]], k = 3
输出:7
解释:
在这个例子中,我们需要选出长度为 3 的子序列。
我们需要选中所有项目。
子序列的总利润为 1 + 2 + 3 = 6,子序列包含 1 种不同类别 [1] 。
因此,最大优雅度为 6 + 12 = 7 。
说明:
- 1 <= items.length == n <= 10^5
- items[i].length == 2
items[i][0] == profitiitems[i][1] == categoryi- 1 <= profiti <= 10^9
- 1 <= categoryi <= n
- 1 <= k <= n
思路
已知一个二维数组,元素为[利润, 种类],数组子序列的优雅值定义为利润和 + 不同种类数量^2,让我们求子序列最大的优雅值是多少。
这道题没有做出来,思考方向错了。刚开始想的是使用记忆化搜索,但是后来发现问题的解不一定能够从子问题得出。即 k-1 子序列的优雅值不一定能够得到 k 子序列的优雅值。
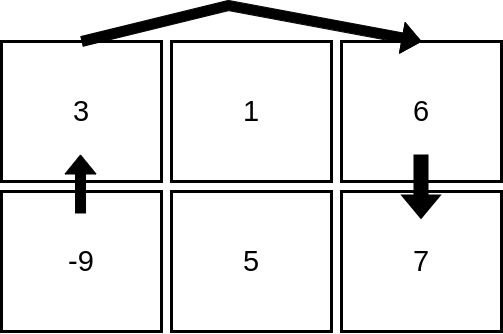
例如:{10, 5} -> {10, 2}, {6, 1}, {9, 5},k = 3,我们先固定第一项,然后从后面取 k 为 2 的优雅值最大子序列 {10, 2}, {9, 5}。但是与第一项结合之后,发现类别有重复的,优雅值为 29 + 4 = 33,小于取 {10, 2}, {6, 1} 得到的优雅值 26 + 9 = 35。
因此使用递归或者动态规划都是不可解的,不能转换成规模更小的子问题。 //2024.06.14 也有可能是可以解的,只不过没有找到正确的切入点。参考访问数组中的位置使分数最大
官网题解使用的是贪心算法,由于后面会对之前的贪心选择做出调整,有网友称为反悔贪心算法。
由于我们求的是优雅值,相对顺序没有影响,因此可以排序。
然后先取最大的k个值,如果其中类别有重复的,尝试用后面的不同类别替换类别重复但利润较小的,直到没有重复的即可。
这是357场周赛的最后一题,2500多分。
代码
//todo