目标
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
示例 1:
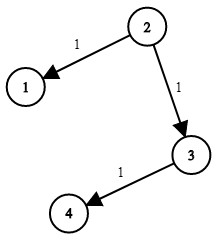
输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出:2示例 2:
输入:times = [[1,2,1]], n = 2, k = 1
输出:1示例 3:
输入:times = [[1,2,1]], n = 2, k = 2
输出:-1说明:
- 1 <= k <= n <= 100
- 1 <= times.length <= 6000
- times[i].length == 3
- 1 <= ui, vi <= n
- ui != vi
- 0 <= wi <= 100
- 所有 (ui, vi) 对都 互不相同(即,不含重复边)
思路
有一个 n 个节点的有向图 ,节点标记为 1 ~ n,求从其中某个节点 k 出发访问到所有其它节点的最短时间。
即从 k 出发求出到达所有其它节点的最短路径,然后取其中的最 大 值。
Floyd 算法的基本思想是动态规划。定义 dp[i][j] 表示从节点 i 到 节点 j 的最短路径,对于所有其它中间节点 m,更新 dp[i][j] = Math.min(dp[i][j], dp[i][m] + dp[m][j]),时间复杂度 O(n^3)。
如果 i -> j 有直接的通路则初始化 dp[i][j] 为路径的权值,否则为 INF。
但是本题不需要其它起点的最短路径,因此可以使用 Dijkstra 算法、Bellman-Ford 算法 或者 SPFA 算法。
图的表示可以使用邻接矩阵、邻接表、前向星、链式前向星等结构。
代码
/**
* @date 2024-11-25 9:08
*/
public class NetworkDelayTime743 {
public int networkDelayTime(int[][] times, int n, int k) {
int[][] dp = new int[n + 1][n + 1];
for (int[] cost : dp) {
Arrays.fill(cost, 20000);
}
for (int[] edge : times) {
dp[edge[0]][edge[1]] = edge[2];
}
for (int m = 1; m <= n; m++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j || i == m || j == m) {
continue;
}
dp[i][j] = Math.min(dp[i][j], dp[i][m] + dp[m][j]);
}
}
}
int res = -1;
for (int i = 1; i <= n; i++) {
if (i == k) {
continue;
}
res = Math.max(dp[k][i], res);
}
return res == 20000 ? -1 : res;
}
}
性能