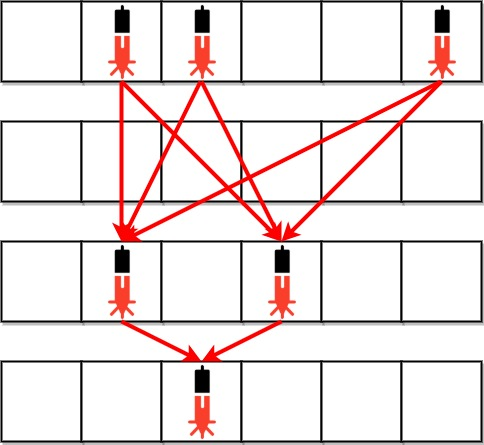
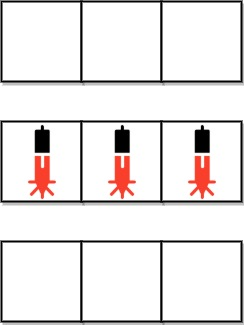
目标
给你一个下标从 0 开始长度为 n 的整数数组 nums 和一个整数 k 。每一次操作中，你可以选择一个数并将它乘 2 。
你最多可以进行 k 次操作，请你返回 nums[0] | nums[1] | ... | nums[n - 1] 的最大值。
a | b 表示两个整数 a 和 b 的 按位或 运算。
示例 1：
输入：nums = [12,9], k = 1
输出：30
解释：如果我们对下标为 1 的元素进行操作，新的数组为 [12,18] 。此时得到最优答案为 12 和 18 的按位或运算的结果，也就是 30 。示例 2：
输入：nums = [8,1,2], k = 2
输出：35
解释：如果我们对下标 0 处的元素进行操作，得到新数组 [32,1,2] 。此时得到最优答案为 32|1|2 = 35 。说明：
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^9
- 1 <= k <= 15
思路
有一个整数数组 nums，最多可以对它执行 k 次操作，每次操作可以任选一个数将其左移 1 位。求操作后数组所有元素的最大或值。
操作集中到同一个数上可以将最高有效位移到最高，少一次操作最高位就低一位。问题的关键在于，如果所有数字都有相同的最高有效位，移哪个是不确定的。
这时就需要枚举操作数了，每选择一个操作数就需要重新计算其余元素的或值。由于或运算没有逆运算，我们无法撤销已经或进去的值。
直接的想法是计算或前缀、后缀，枚举所有元素，将其左移 k 次，然后与前后缀进行或运算，取最大值。
网友提供了另一种基于位运算的解法，计算全体元素的或值，同时计算所有 bit 位上存在重复 1 的位置，通过异或运算将当前元素对或值的贡献抵消，然后补上重复位置上的 1。
代码
/**
* @date 2025-03-21 0:08
*/
public class MaximumOr2680 {
public long maximumOr_v1(int[] nums, int k) {
int n = nums.length;
int or = 0;
int multiBits = 0;
for (int i = 0; i < n; i++) {
multiBits = multiBits | or & nums[i];
or = or | nums[i];
}
long res = 0L;
for (int i = 0; i < n; i++) {
res = Math.max(res, or ^ nums[i] | multiBits | ((long) nums[i] << k));
}
return res;
}
public long maximumOr(int[] nums, int k) {
int n = nums.length;
int[] prefix = new int[n + 1];
int[] suffix = new int[n + 1];
for (int i = 1; i <= n; i++) {
prefix[i] = prefix[i - 1] | nums[i - 1];
suffix[n - i] = suffix[n - i + 1] | nums[n - i];
}
long res = 0L;
for (int i = 0; i < n; i++) {
res = Math.max(res, prefix[i] | suffix[i + 1] | ((long) nums[i] << k));
}
return res;
}
}
性能
