目标
给你一个下标从 0 开始的二维整数数组 events ,其中 events[i] = [startTimei, endTimei, valuei] 。第 i 个活动开始于 startTimei ,结束于 endTimei ,如果你参加这个活动,那么你可以得到价值 valuei 。你 最多 可以参加 两个时间不重叠 活动,使得它们的价值之和 最大 。
请你返回价值之和的 最大值 。
注意,活动的开始时间和结束时间是 包括 在活动时间内的,也就是说,你不能参加两个活动且它们之一的开始时间等于另一个活动的结束时间。更具体的,如果你参加一个活动,且结束时间为 t ,那么下一个活动必须在 t + 1 或之后的时间开始。
示例 1:

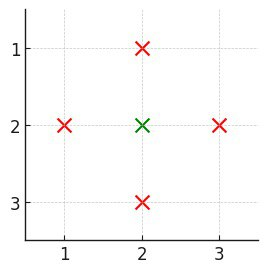
输入:events = [[1,3,2],[4,5,2],[2,4,3]]
输出:4
解释:选择绿色的活动 0 和 1 ,价值之和为 2 + 2 = 4 。示例 2:

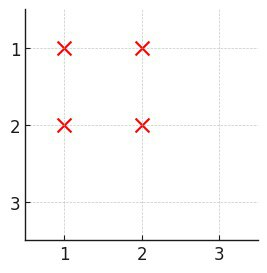
输入:events = [[1,3,2],[4,5,2],[1,5,5]]
输出:5
解释:选择活动 2 ,价值和为 5 。示例 3:

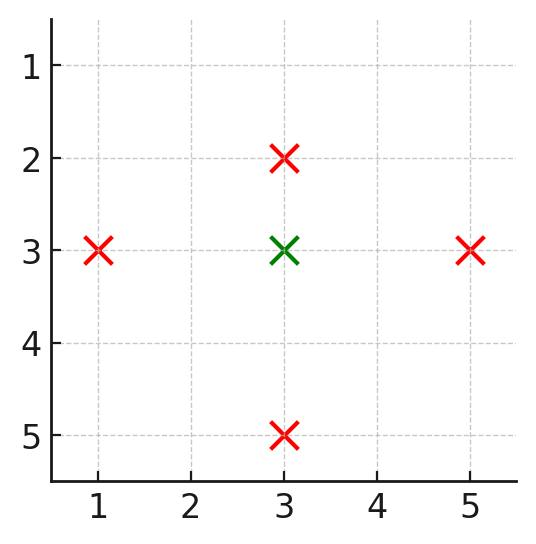
输入:events = [[1,5,3],[1,5,1],[6,6,5]]
输出:8
解释:选择活动 0 和 2 ,价值之和为 3 + 5 = 8 。说明:
- 2 <= events.length <= 10^5
- events[i].length == 3
- 1 <= startTimei <= endTimei <= 10^9
- 1 <= valuei <= 10^6
思路
有一个二维数组 events,events[i] 表示事件 i 的 (开始时间,结束时间,价值) 三元组,至多参加两个活动,这两个活动不能重叠 (结束时间与开始时间也不能重叠),求参加活动的最大价值。
根据开始时间排序,二分查找第一个大于结束时间的下标,维护后缀最大值。
代码
/**
* @date 2025-12-23 8:53
*/
public class MaxTwoEvents2054 {
public int maxTwoEvents(int[][] events) {
Arrays.sort(events, (a, b) -> a[0] - b[0]);
int res = 0;
int n = events.length;
int[] suffix = new int[n + 1];
for (int i = n - 1; i >= 0; i--) {
suffix[i] = Math.max(suffix[i + 1], events[i][2]);
}
for (int[] event : events) {
int index = bs(events, event[1]);
res = Math.max(res, event[2] + suffix[index]);
}
return res;
}
public int bs(int[][] events, int target) {
int l = 0;
int r = events.length - 1;
int m = l + (r - l) / 2;
while (l <= r) {
if (events[m][0] <= target) {
l = m + 1;
} else {
r = m - 1;
}
m = l + (r - l) / 2;
}
return l;
}
}
性能