标签： medium

目标

给你一个正整数数组 values，其中 values[i] 表示第 i 个观光景点的评分，并且两个景点 i 和 j 之间的 距离 为 j - i。

一对景点（i < j）组成的观光组合的得分为 values[i] + values[j] + i - j ，也就是景点的评分之和 减去 它们两者之间的距离。

返回一对观光景点能取得的最高分。

示例 1：

输入：values = [8,1,5,2,6]
输出：11
解释：i = 0, j = 2, values[i] + values[j] + i - j = 8 + 5 + 0 - 2 = 11

示例 2：

输入：values = [1,2]
输出：2

说明：

• 2 <= values.length <= 5 * 10^4
• 1 <= values[i] <= 1000

思路

从数组 values 中选两个下标，计算 values[i] + values[j] + i - j 的最大值。

遍历可能组合的复杂度为 O(n^2)，暴力求解不可行。很自然地想动态规划，考虑重复子问题是什么？如果是累加 i ~ j 范围内的 value，然后再加上 i - j，由于 value[i] >= 1，当 j 固定的时候，i 应该尽可能的小，因为累加 value[i] 抵消了 i 的减少。但这里并不是累加所有景点的评分，而是选两个景点，然后再考虑它们之间的距离。

注意到，当 j 固定时，评分的最大值即为 value[i] + i 的最大值。当 i 固定时，评分最大值为 values[j] - j 的最大值。但是我们不能直接取这两个最大值相加，需要保证 i 取得最大值时，i < j。枚举右边界，计算之前的最大值。

定义 dp[i] 表示 [0, i] 范围内， value[i] + i 的最大值。那么评分的最大值即为 value[j] - j + dp[j - 1] 的最大值。由于只与 dp[j - 1] 有关，可以进行空间优化，用一个变量保存截止到前一个元素的最大值。

这里面有一个小技巧是将 maxi 放到后面更新，这样就不用维护 i = j - 1 这个指针了。

代码

/**
 * @date 2024-09-23 9:26
 */
public class MaxScoreSightseeingPair1014 {

    public int maxScoreSightseeingPair(int[] values) {
        int n = values.length;
        int maxi = values[0];
        int res = 0;
        for (int j = 1; j < n; j++) {
            res = Math.max(res, values[j] - j + maxi);
            maxi = Math.max(maxi, values[j] + j);
        }
        return res;
    }

}

性能

目标

给你一个包含若干星号 * 的字符串 s 。

在一步操作中，你可以：

• 选中 s 中的一个星号。
• 移除星号 左侧 最近的那个 非星号 字符，并移除该星号自身。

返回移除 所有 星号之后的字符串。

注意：

• 生成的输入保证总是可以执行题面中描述的操作。
• 可以证明结果字符串是唯一的。

示例 1：

输入：s = "leet**cod*e"
输出："lecoe"
解释：从左到右执行移除操作：
- 距离第 1 个星号最近的字符是 "leet**cod*e" 中的 't' ，s 变为 "lee*cod*e" 。
- 距离第 2 个星号最近的字符是 "lee*cod*e" 中的 'e' ，s 变为 "lecod*e" 。
- 距离第 3 个星号最近的字符是 "lecod*e" 中的 'd' ，s 变为 "lecoe" 。
不存在其他星号，返回 "lecoe" 。

示例 2：

输入：s = "erase*****"
输出：""
解释：整个字符串都会被移除，所以返回空字符串。

说明：

• 1 <= s.length <= 10^5
• s 由小写英文字母和星号 * 组成
• s 可以执行上述操作

思路

移除字符串中的星号以及星号左侧的非星号字符。

直接模拟栈的行为即可，可以使用StringBuilder，遇到星号就删除最后一个字符。

deleteCharAt(index) 实际上调用的是 System.arraycopy(value, index+1, value, index, count-index-1); 将index后的数据前移了一位。这里删除的是最后一个字符，实际上就是将指针向前移了一位。那我们可以直接将指针向前移，省去这一系列的函数调用。

可以直接原地修改，定义一个指针 p 与 i 同步增长，如果遇到 *， 指针 p 回退，否则将下标 i 对应的值写入当前 p 指向的位置。

代码

/**
 * @date 2024-09-14 8:56
 */
public class RemoveStars2390 {

    public String removeStars_v2(String s) {
        char[] chars = s.toCharArray();
        int n = chars.length;
        int p = 0;
        for (int i = 0; i < n; i++) {
            if (chars[i] == '*') {
                p--;
            } else {
                chars[p++] = chars[i];
            }
        }
        return new String(chars, 0, p);
    }

}

性能

目标

给你一个下标从 0 开始的整数数组 nums 。

一开始，所有下标都没有被标记。你可以执行以下操作任意次：

• 选择两个 互不相同且未标记 的下标 i 和 j ，满足 2 * nums[i] <= nums[j] ，标记下标 i 和 j 。

请你执行上述操作任意次，返回 nums 中最多可以标记的下标数目。

示例 1：

输入：nums = [3,5,2,4]
输出：2
解释：第一次操作中，选择 i = 2 和 j = 1 ，操作可以执行的原因是 2 * nums[2] <= nums[1] ，标记下标 2 和 1 。
没有其他更多可执行的操作，所以答案为 2 。

示例 2：

输入：nums = [9,2,5,4]
输出：4
解释：第一次操作中，选择 i = 3 和 j = 0 ，操作可以执行的原因是 2 * nums[3] <= nums[0] ，标记下标 3 和 0 。
第二次操作中，选择 i = 1 和 j = 2 ，操作可以执行的原因是 2 * nums[1] <= nums[2] ，标记下标 1 和 2 。
没有其他更多可执行的操作，所以答案为 4 。

示例 3：

输入：nums = [7,6,8]
输出：0
解释：没有任何可以执行的操作，所以答案为 0 。

说明：

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^9

提示：

• Think about how to check that performing k operations is possible.
• To perform k operations, it’s optimal to use the smallest k elements and the largest k elements and think about how to match them.
• It’s optimal to match the ith smallest number with the k-i + 1 largest number.
• Now we need to binary search on the answer and find the greatest possible valid k.

思路

有一个数组 nums，每一次操作我们可以标记数组中未被标记的两个数，要求其中一个数的两倍小于等于另一个数。问经过任意次操作，最多可以标记多少个数。

题目与下标无关，可以先排序。使用双指针 l r 从前往后找到第一个大于等于其两倍的数 p。然后 l+1 r 继续向后搜索，直到 l 到达 p，这时将 l 赋值为 r，并且赋值 r = r + 1，继续前面的算法。 应该使用一个数组记录是否已标记，当 l 第一次到达 p 时，应跳转到之前 r 未被标记的下标。

这种贪心策略也是不对的，对于示例2，排序后的数组为 2 4 5 9。如果优先标记 2 4 后面就不能再标记了，而如果先标记 2 5 我们还可以标记 4 9。

那如果我们倒过来考虑呢？从后往前找试试。反过来也不对，例如 10 10 40 100 如果先标记 40 100 前面就不能再标记了。

这样一来我们不知道满足条件后是否应该标记，需要搜索解空间看看哪个最大。回溯搜索相当于搜索n叉树 O(n^n)，如果不进行剪枝或者记忆的话肯定超时。如果考虑动态规划，状态又比较多，取决于元素是否被标记。

看了提示，匹配策略一定是前 k 个小的 small[i] 与后 k 个大的 big[i] 匹配。还是上面的例子 2 4 | 5 9 10 10 | 40 100 最优的匹配方式就是 2 5 4 9 10 40 10 100。现在问题就变成了找出最大的 k。使用二分法查找满足条件的最大 k，然后返回 2k 就是答案。

这道题卡住的点是没想清楚匹配方式。先入为主地以滑动窗口的方式匹配，连续地比较，匹配第一个能够匹配的，这种策略是不对的。

更优的解法是直接用双指针遍历，因为二分查找的判断复杂度为O(k)，整体是O(klogn)，不如双指针的O(n)。

代码

/**
 * @date 2024-09-12 9:14
 */
public class MaxNumOfMarkedIndices2576 {

    /**
     * 排序的复杂度O(nlogn) 双指针匹配的复杂度O((n + 1) / 2)
     */
    public int maxNumOfMarkedIndices_v1(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        int rs = (n + 1) / 2;
        int l = 0;
        for (int r = rs; r < n; r++) {
            if (nums[l] * 2 <= nums[r]) {
                l++;
            }
        }
        return 2 * l;
    }

    /**
     * 排序的复杂度O(nlogn) 二分查找复杂度O(klogn) 其中判断的复杂度O(k) k最坏的情况下取n/2
     */
    public int maxNumOfMarkedIndices(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        int l = 0, r = n / 2, k = l + (r - l) / 2;
        while (l <= r) {
            if (check(nums, k)) {
                l = k + 1;
            } else {
                r = k - 1;
            }
            k = l + (r - l) / 2;
        }
        return 2 * r;
    }

    public boolean check(int[] nums, int k) {
        int n = nums.length;
        for (int i = 0; i < k; i++) {
            if (nums[i] * 2 > nums[n - k + i]) {
                return false;
            }
        }
        return true;
    }

}

性能

二分查找

双指针

目标

在 X轴 上有一些奖品。给你一个整数数组 prizePositions ，它按照 非递减 顺序排列，其中 prizePositions[i] 是第 i 件奖品的位置。数轴上一个位置可能会有多件奖品。再给你一个整数 k 。

你可以选择两个端点为整数的线段。每个线段的长度都必须是 k 。你可以获得位置在任一线段上的所有奖品（包括线段的两个端点）。注意，两个线段可能会有相交。

• 比方说 k = 2 ，你可以选择线段 [1, 3] 和 [2, 4] ，你可以获得满足 1 <= prizePositions[i] <= 3 或者 2 <= prizePositions[i] <= 4 的所有奖品 i 。

请你返回在选择两个最优线段的前提下，可以获得的 最多 奖品数目。

示例 1：

输入：prizePositions = [1,1,2,2,3,3,5], k = 2
输出：7
解释：这个例子中，你可以选择线段 [1, 3] 和 [3, 5] ，获得 7 个奖品。

示例 2：

输入：prizePositions = [1,2,3,4], k = 0
输出：2
解释：这个例子中，一个选择是选择线段 [3, 3] 和 [4, 4] ，获得 2 个奖品。

说明：

• 1 <= prizePositions.length <= 10^5
• 1 <= prizePositions[i] <= 10^9
• 0 <= k <= 10^9
• prizePositions 有序非递减。

思路

x轴的一些整数坐标上放有奖品，相同坐标点上可能有多个奖品。已知所有奖品所在坐标从小到大排序后的数组 prizePositions，问使用两个长度为k的线段最多能覆盖多少个奖品。线段可以相交，但相交区间内的奖品仅计数一次，线段端点处的奖品也计入总数。

最直观的想法是使用滑动窗口，固定区间长度，然后求能够覆盖的最多奖品数。但我们需要的是两个线段所能覆盖的最多奖品，能否记录下第一次求得的区间范围，然后在范围之外（两个线段尽量不相交才能覆盖更多奖品）在用相同的方法求次最多的奖品数。这看上去似乎可行，但具体写完之后会发现一些问题。

• 如果存在多个最大区间如何处理？可以参考下图，k取3的情况，不同的选择直接影响另一线段的取值。可以用一个列表记录区间范围，然后分别对这些区间范围之外的区间执行同样的算法？时间复杂度为 O(m * l)，m 为最大线段个数，l 为区间长度。

  

• 就算上面的复杂度可以接受，两个线段获得最多奖品，一定要其中一个线段覆盖最多的奖品吗？这个是不必要的。参考下图，k取2的情况：

  

针对这道题，这种贪心策略是不行的，局部最优解并不一定是全局最优解。现在我们没有一个明确的目标，最优的线段该如何取？如果我们同时滑动两个窗口呢？暴力写法是先固定一个，然后滑动另一个。时间复杂度为 O(n^2)，肯定超时。我们发现这里面有重复的子问题，定义 num[i] 表示以 prizePositions[i] 为起点长度为 k 的线段所能覆盖的奖品数。然后再用一个 max[i] 表示起点大于等于 prizePositions[i] 长度为 k 的线段所能覆盖的最大奖品数。这样我们就能以 O(1) 的复杂度取到固定一个窗口之后，另一个窗口的最大值。枚举固定窗口求出最大值即可。

写完之后发现，保存 num[i] 是不必要的，它只用来更新当前的 max[i]。

滑动窗口有两种写法，枚举左边界，循环内部直接到达可能的最右边界。另一种写法是枚举右边界，如果条件不满足，更新左边界直到满足条件。注意确保不要越界。

官网题解提供了二分法的解法，确实遇到有序数组就要想到二分法，但是这里二分找什么呢？大概是二分找所能覆盖的左边界，然后还是动态规划求不超过左边界的另一线段所能覆盖的最大值。官方题解这个解法的java版本好像是其它题目的，给错答案了。

代码

/**
 * @date 2024-09-11 8:57
 */
public class MaximizeWin2555 {

    public int maximizeWin_v1(int[] prizePositions, int k) {
        int n = prizePositions.length;
        if (k * 2 + 1 >= prizePositions[n - 1] - prizePositions[0]) {
            return n;
        }
        int res = 1;
        int[] max = new int[n + 1];
        int l = n - 1;
        for (int r = n - 1; r >= 0; r--) {
            while (l >= 0 && prizePositions[r] - prizePositions[l] <= k) {
                max[l] = Math.max(r - l + 1, max[l + 1]);
                res = Math.max(res, r - l + 1 + max[r + 1]);
                l--;
            }
        }
        return res;
    }

}

性能

目标

给你一个整数数组 nums 和一个 非负 整数 k 。如果一个整数序列 seq 满足在范围下标范围 [0, seq.length - 2] 中存在 不超过 k 个下标 i 满足 seq[i] != seq[i + 1] ，那么我们称这个整数序列为 好 序列。

请你返回 nums 中 好 子序列 的最长长度

示例 1：

输入：nums = [1,2,1,1,3], k = 2
输出：4
解释：
最长好子序列为 [1,2,1,1] 。

示例 2：

输入：nums = [1,2,3,4,5,1], k = 0
输出：2
解释：
最长好子序列为 [1,1] 。

说明：

• 1 <= nums.length <= 500
• 1 <= nums[i] <= 10^9
• 0 <= k <= min(nums.length, 25)

提示：

• The absolute values in nums don’t really matter. So we can remap the set of values to the range [0, n - 1].
• Let dp[i][j] be the length of the longest subsequence till index j with at most i positions such that seq[i] != seq[i + 1].
• For each value x from left to right, update dp[i][x] = max(dp[i][x] + 1, dp[i - 1][y] + 1), where y != x.

思路

求整数数组 nums 的子序列，要求子序列中最多存在 k 个下标 i 满足 seq[i] != seq[i + 1]，即至多 k 对相邻元素 不同。

只要选出了子序列，那么相邻元素 不同 的对数就已经确定。

记忆化搜索超时了 // todo

代码

性能

目标

给你一个下标从 0 开始、长度为 n 的整数数组 nums ，其中 n 是班级中学生的总数。班主任希望能够在让所有学生保持开心的情况下选出一组学生：

如果能够满足下述两个条件之一，则认为第 i 位学生将会保持开心：

• 这位学生被选中，并且被选中的学生人数 严格大于 nums[i] 。
• 这位学生没有被选中，并且被选中的学生人数 严格小于 nums[i] 。

返回能够满足让所有学生保持开心的分组方法的数目。

示例 1：

输入：nums = [1,1]
输出：2
解释：
有两种可行的方法：
班主任没有选中学生。
班主任选中所有学生形成一组。 
如果班主任仅选中一个学生来完成分组，那么两个学生都无法保持开心。因此，仅存在两种可行的方法。

示例 2：

输入：nums = [6,0,3,3,6,7,2,7]
输出：3
解释：
存在三种可行的方法：
班主任选中下标为 1 的学生形成一组。
班主任选中下标为 1、2、3、6 的学生形成一组。
班主任选中所有学生形成一组。

说明：

• 1 <= nums.length <= 10^5
• 0 <= nums[i] < nums.length

思路

从数组中选择一组元素，使之满足该组元素个数严格大于组中所有元素值并且严格小于未被选择的元素值，求满足条件的所有选择数。

注意到元素值不超过数组长度，可以先统计各元素值的出现次数 cnt[i]，然后遍历 cnt。

这道题的关键是要意识到：值相同的元素要么同时被选，要么同时不被选。因为选择的元素个数 sum 应该大于所有选择的元素值，小于所有未选择的元素值，一个元素不可能既小于 sum 又大于 sum。题目的本质是将学生成两组（被选择的和未被选择的），选择的标准是根据所选人数动态变化的，水平相同的学生要么都选，要么都不选，要一碗水端平，这就是题目名想要表达的处世哲学吧。

• 当 cnt[0] == 0 时，说明所有元素都大于0，因此可以一个都不选。
• 当 cnt[i] != 0 时，如果我们想要选择这些元素值为i的学生，需要满足选择后的学生总数 sum 大于 i，并且 cnt[i+1] ~ cnt[sum] 应该都为0，否则就存在小于 sum 但是未被选的学生了。

官网题解使用的是排序，满足 sorted[i - 1] < i && i < sorted[i] 时累加计数。不过排序的复杂度是O(nlogn)，其实我们的计数数组也是有序的，算是计数排序吧，时间复杂度为O(n)。

代码

/**
 * @date 2024-09-04 10:29
 */
public class CountWays2860 {
    public int countWays(List<Integer> nums) {
        int n = nums.size();
        int[] cnt = new int[n];
        for (Integer num : nums) {
            cnt[num]++;
        }
        int[] prefix = new int[n];
        for (int i = 1; i < n; i++) {
            prefix[i] = prefix[i - 1] + cnt[i];
        }
        int res = cnt[0] > 0 ? 0 : 1;
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += cnt[i];
            if (sum > i && cnt[i] != 0 && prefix[Math.min(n - 1, sum)] == prefix[i]) {
                res++;
            }
        }
        return res;
    }
}

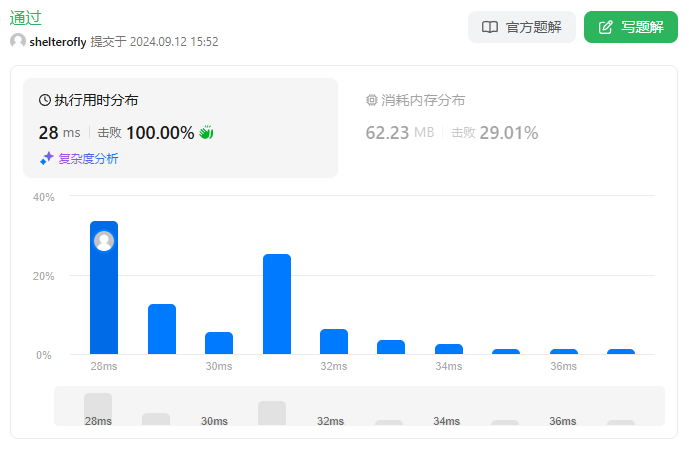
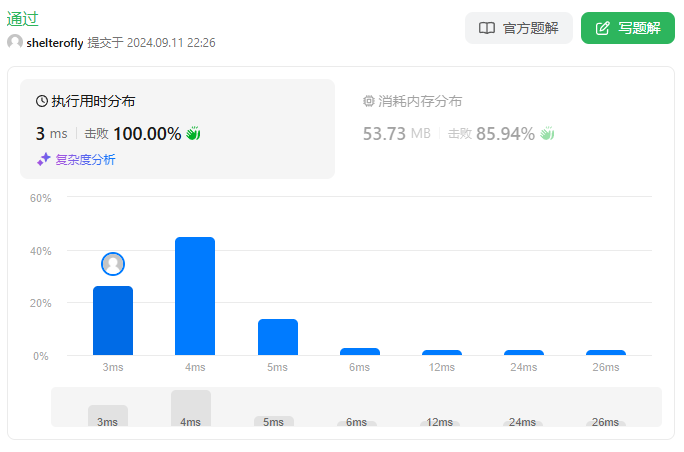
性能