目标
给你 2 枚相同 的鸡蛋,和一栋从第 1 层到第 n 层共有 n 层楼的建筑。
已知存在楼层 f ,满足 0 <= f <= n ,任何从 高于 f 的楼层落下的鸡蛋都 会碎 ,从 f 楼层或比它低 的楼层落下的鸡蛋都 不会碎 。
每次操作,你可以取一枚 没有碎 的鸡蛋并把它从任一楼层 x 扔下(满足 1 <= x <= n)。如果鸡蛋碎了,你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎,则可以在之后的操作中 重复使用 这枚鸡蛋。
请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少?
示例 1:
输入:n = 2
输出:2
解释:我们可以将第一枚鸡蛋从 1 楼扔下,然后将第二枚从 2 楼扔下。
如果第一枚鸡蛋碎了,可知 f = 0;
如果第二枚鸡蛋碎了,但第一枚没碎,可知 f = 1;
否则,当两个鸡蛋都没碎时,可知 f = 2。示例 2:
输入:n = 100
输出:14
解释:
一种最优的策略是:
- 将第一枚鸡蛋从 9 楼扔下。如果碎了,那么 f 在 0 和 8 之间。将第二枚从 1 楼扔下,然后每扔一次上一层楼,在 8 次内找到 f 。总操作次数 = 1 + 8 = 9 。
- 如果第一枚鸡蛋没有碎,那么再把第一枚鸡蛋从 22 层扔下。如果碎了,那么 f 在 9 和 21 之间。将第二枚鸡蛋从 10 楼扔下,然后每扔一次上一层楼,在 12 次内找到 f 。总操作次数 = 2 + 12 = 14 。
- 如果第一枚鸡蛋没有再次碎掉,则按照类似的方法从 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99 和 100 楼分别扔下第一枚鸡蛋。
不管结果如何,最多需要扔 14 次来确定 f 。说明:
- 1 <= n <= 1000
思路
有一个 1 ~ n 层楼的建筑,存在一个楼层 f,任何大于 f 层落下的鸡蛋都会摔碎。现在有两个鸡蛋,每次操作可以从任意楼层向下扔鸡蛋,如果鸡蛋碎了则无法再使用,求确定 f 值的最小操作次数。
为了确保能够找到 f,如果第一个尝试的鸡蛋碎了,那么另一个鸡蛋只能从已知的安全楼层一层一层向上尝试。
观察示例2,可以从 n 开始 减 1 2 3 …… i 直到小于等于零,返回 i - 1即可。
看了题解,这样做可行的逻辑是这样的:
假设已知最小操作次数 k,我们扔第一枚鸡蛋选第几层?显然,应该选第 k 层,因为如果第一枚鸡蛋碎了,只需要从 1 ~ k - 1 枚举即可。
如果第一枚鸡蛋没碎,那么下一次选第几层?现在还剩下 k - 1 次尝试,所以应该选 k + 1 + (k - 2) = k + (k - 1) 层,因为如果在该层扔鸡蛋碎了,只需从 k + 1 ~ k + k - 2 枚举即可,共 k - 2 次,再加上前面尝试的 2 次,总次数为 k。
以此类推,我们可以确定总层数 n = k + (k - 1) + (k - 2) + …… + 2 + 1 = k * (k + 1)/2,解方程得 k = (sqrt(1+8*n) - 1)/2,结果需要向上取整。
代码
/**
* @date 2024-10-13 19:30
*/
public class TwoEggDrop1884 {
public int twoEggDrop_v1(int n) {
return (int) Math.ceil((Math.sqrt(1 + 8 * n) - 1) / 2);
}
public int twoEggDrop(int n) {
int i = 1;
while (n > 0){
n -= i++;
}
return i - 1;
}
}
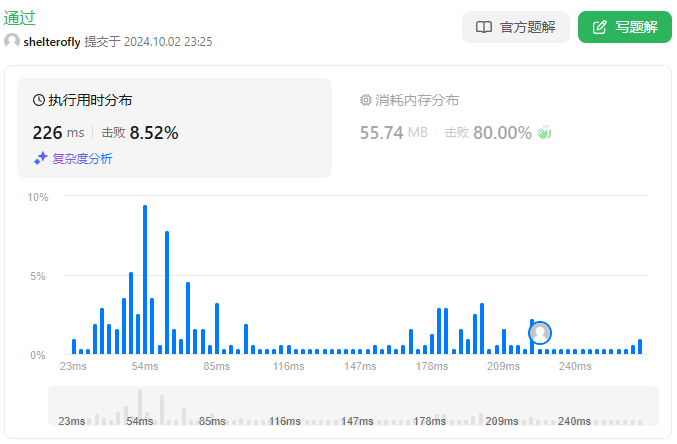
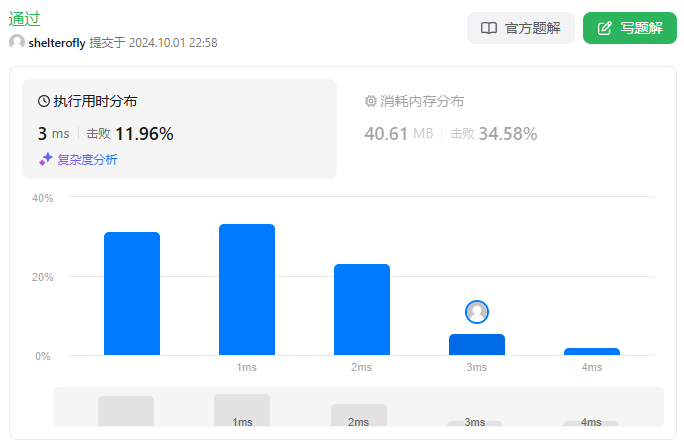
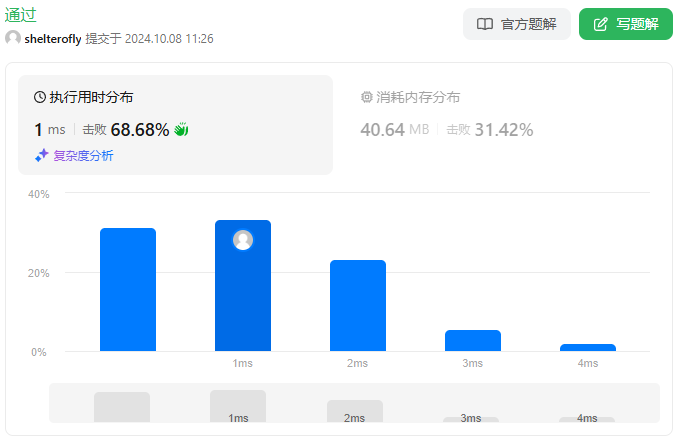
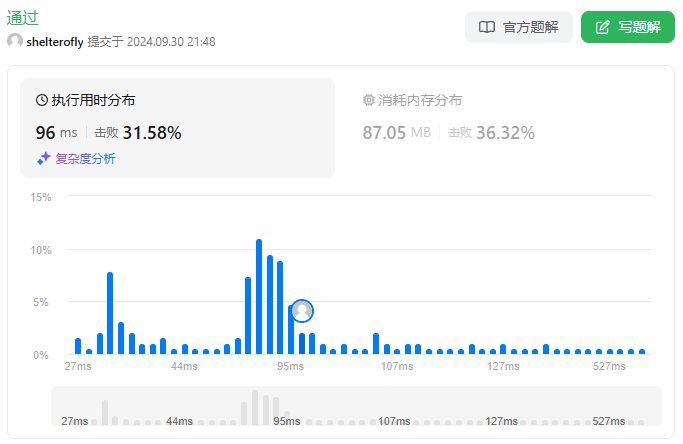
性能