目标
实现一个程序来存放你的日程安排。如果要添加的时间内不会导致三重预订时,则可以存储这个新的日程安排。
当三个日程安排有一些时间上的交叉时(例如三个日程安排都在同一时间内),就会产生 三重预订。
事件能够用一对整数 startTime 和 endTime 表示,在一个半开区间的时间 [startTime, endTime) 上预定。实数 x 的范围为 startTime <= x < endTime。
实现 MyCalendarTwo 类:
- MyCalendarTwo() 初始化日历对象。
- boolean book(int startTime, int endTime) 如果可以将日程安排成功添加到日历中而不会导致三重预订,返回 true。否则,返回 false 并且不要将该日程安排添加到日历中。
示例 1:
输入:
["MyCalendarTwo", "book", "book", "book", "book", "book", "book"]
[[], [10, 20], [50, 60], [10, 40], [5, 15], [5, 10], [25, 55]]
输出:
[null, true, true, true, false, true, true]
解释:
MyCalendarTwo myCalendarTwo = new MyCalendarTwo();
myCalendarTwo.book(10, 20); // 返回 True,能够预定该日程。
myCalendarTwo.book(50, 60); // 返回 True,能够预定该日程。
myCalendarTwo.book(10, 40); // 返回 True,该日程能够被重复预定。
myCalendarTwo.book(5, 15); // 返回 False,该日程导致了三重预定,所以不能预定。
myCalendarTwo.book(5, 10); // 返回 True,能够预定该日程,因为它不使用已经双重预订的时间 10。
myCalendarTwo.book(25, 55); // 返回 True,能够预定该日程,因为时间段 [25, 40) 将被第三个日程重复预定,时间段 [40, 50) 将被单独预定,而时间段 [50, 55) 将被第二个日程重复预定。说明:
- 0 <= start < end <= 10^9
- 最多调用 book 1000 次。
思路
本题与 729.我的日程安排表I 的区别是允许相交一次。
使用差分数组记录区间元素被覆盖的次数,由于数据范围太大,这里使用 TreeMap 计数。
// todo 线段树
代码
/**
* @date 2025-01-03 10:32
*/
public class MyCalendarTwo {
TreeMap<Integer, Integer> cnt = new TreeMap<>();
public MyCalendarTwo() {
}
public boolean book(int startTime, int endTime) {
cnt.put(startTime, cnt.getOrDefault(startTime, 0) + 1);
cnt.put(endTime, cnt.getOrDefault(endTime, 0) - 1);
int appearanceCnt = 0;
for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
int key = entry.getKey();
int value = entry.getValue();
if (key >= endTime) {
break;
}
appearanceCnt += value;
if (appearanceCnt > 2) {
cnt.put(startTime, cnt.getOrDefault(startTime, 0) - 1);
cnt.put(endTime, cnt.getOrDefault(endTime, 0) + 1);
return false;
}
}
return true;
}
}
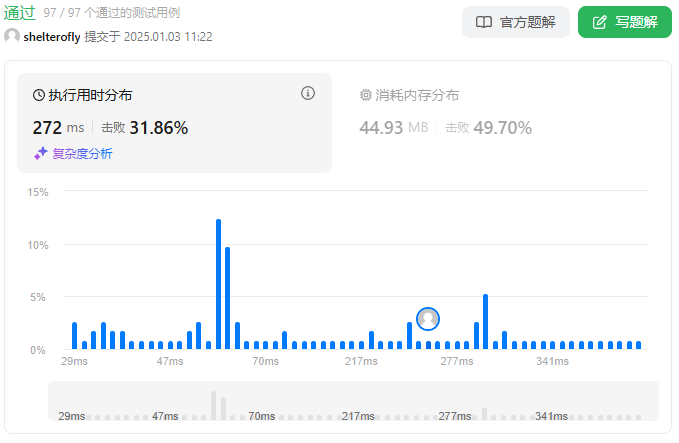
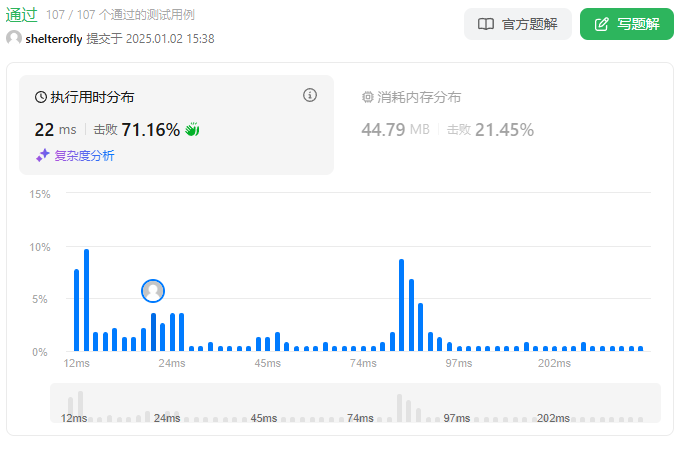
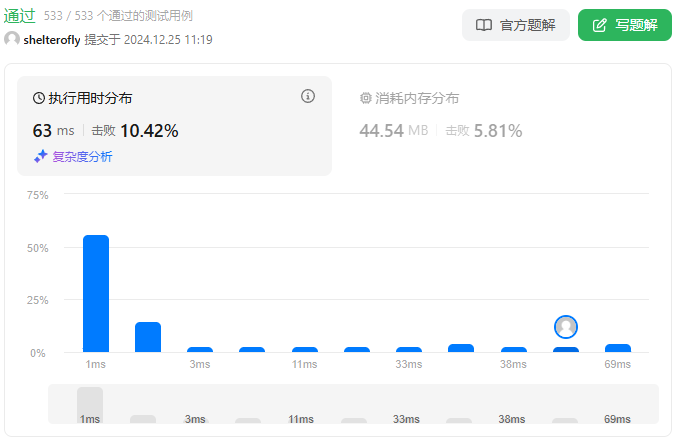
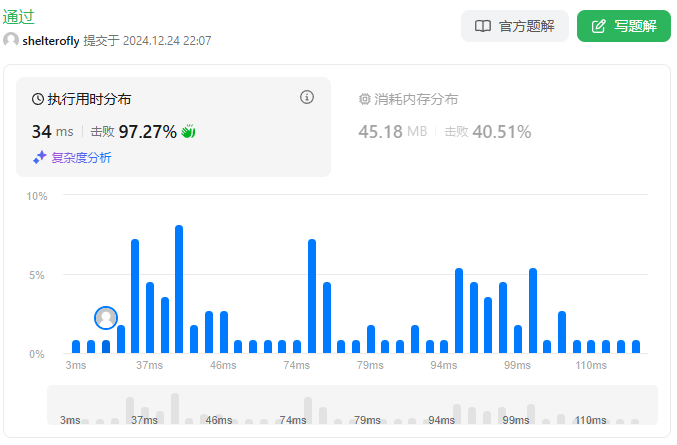
性能