目标
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示,表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边,那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号,使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1 。
注意 edges 可能包含环。
示例 1:
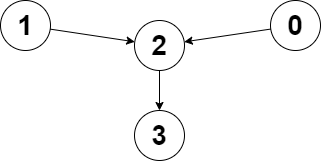
输入:edges = [2,2,3,-1], node1 = 0, node2 = 1
输出:2
解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。示例 2:
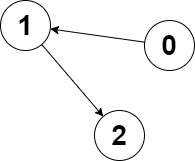
输入:edges = [1,2,-1], node1 = 0, node2 = 2
输出:2
解释:节点 0 到节点 2 的距离为 2 ,节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值,所以我们返回节点 2 。说明:
- n == edges.length
- 2 <= n <= 10^5
- -1 <= edges[i] < n
- edges[i] != i
- 0 <= node1, node2 < n
思路
使用两个不同的起点公用一个dfs,出度最大为 1,使用两个集合记录访问路径,遇到环、共同访问过的节点或者出度为 0 则停止。
代码
/**
* @date 2025-05-30 0:44
*/
public class ClosestMeetingNode2359 {
public int closestMeetingNode(int[] edges, int node1, int node2) {
return dfs(node1, node2, edges, new HashSet<>(), new HashSet<>());
}
public int dfs(int cur1, int cur2, int[] edges, Set<Integer> set1, Set<Integer> set2) {
if (set1.contains(cur2) && set2.contains(cur1) || cur1 == cur2) {
return Math.min(cur1, cur2);
} else if (set1.contains(cur2)) {
return cur2;
} else if (set2.contains(cur1)) {
return cur1;
}
if (cur1 != -1) {
set1.add(cur1);
}
if (cur2 != -1) {
set2.add(cur2);
}
if (cur1 != -1 && !set1.contains(edges[cur1])) {
return dfs(edges[cur1], cur2 == -1 ? -1 : edges[cur2], edges, set1, set2);
} else if (cur2 != -1 && !set2.contains(edges[cur2])) {
return dfs(cur1 == -1 ? -1 : edges[cur1], edges[cur2], edges, set1, set2);
}
return -1;
}
}
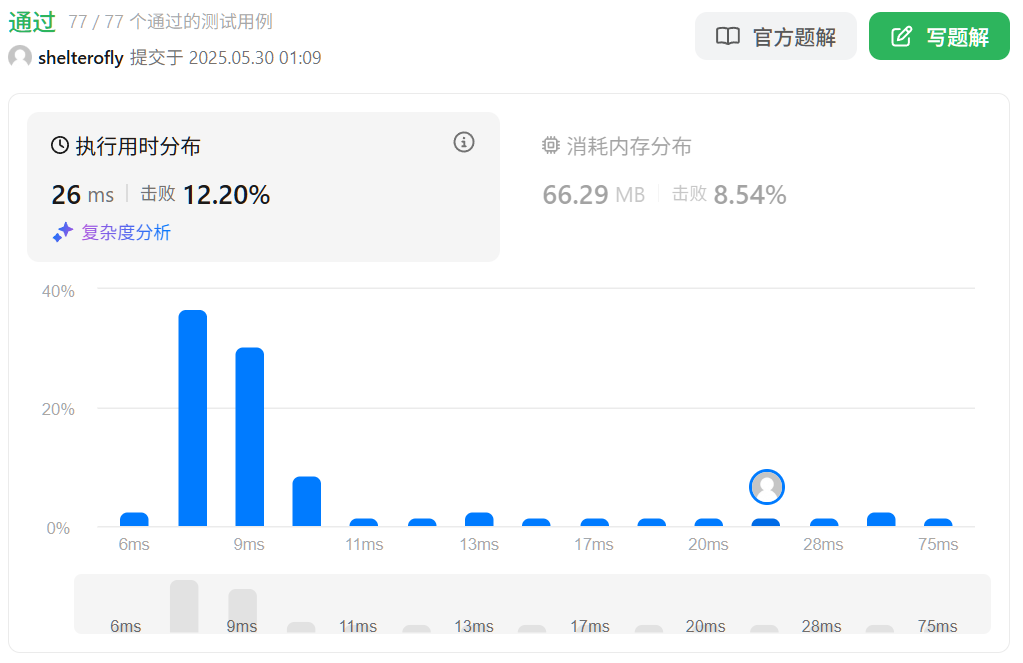
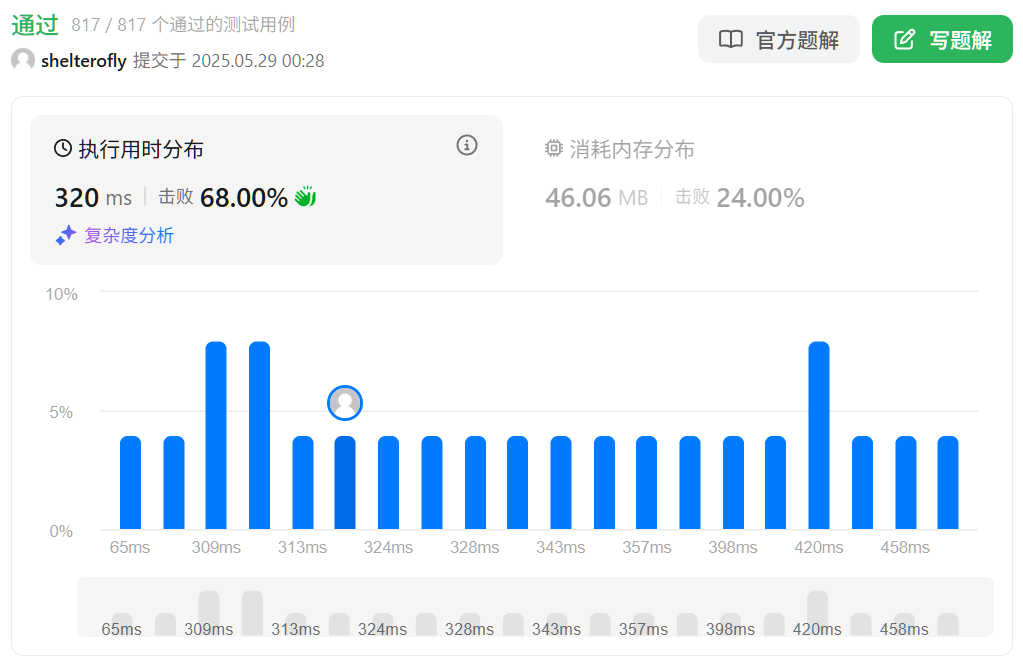
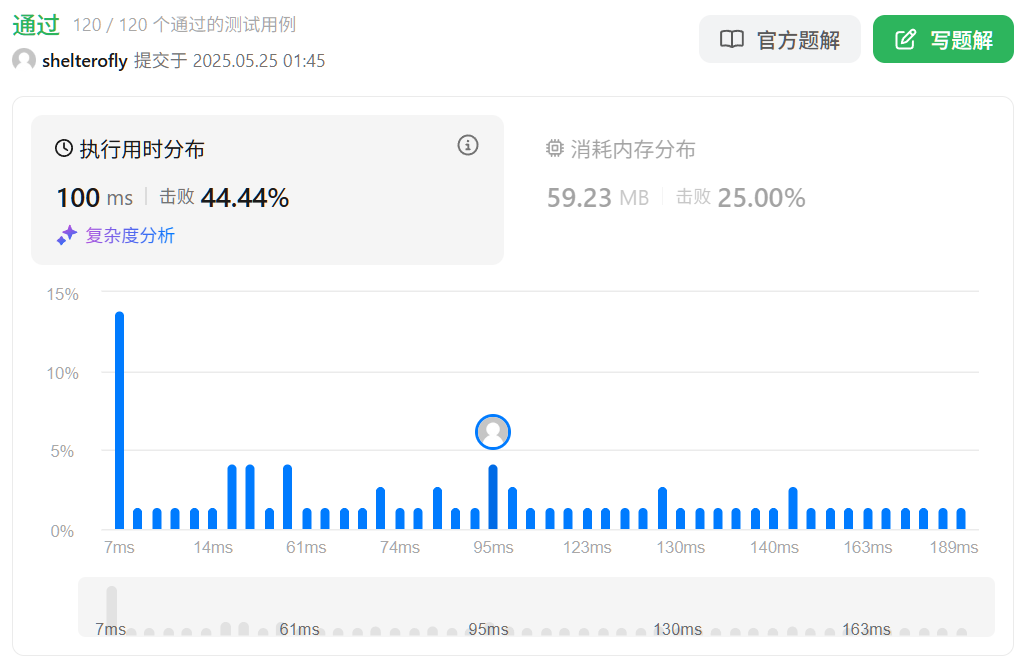
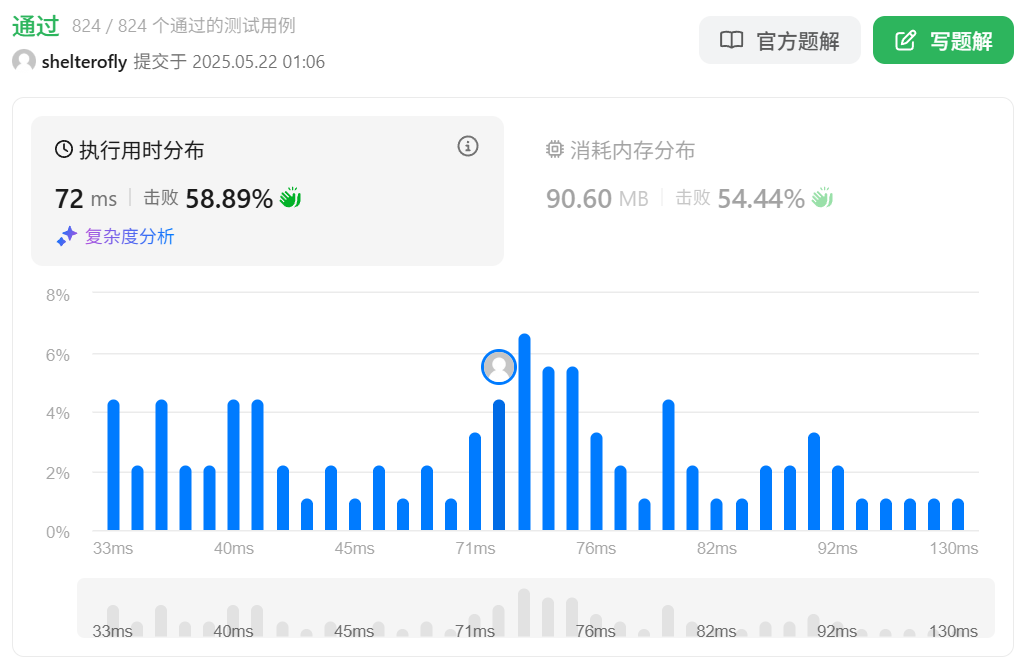
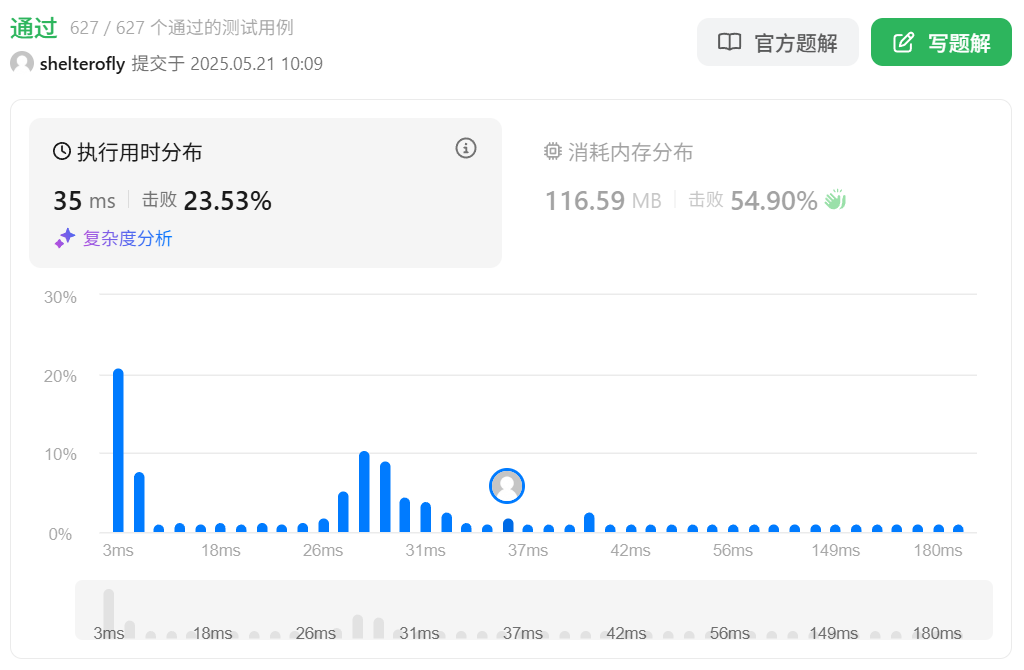
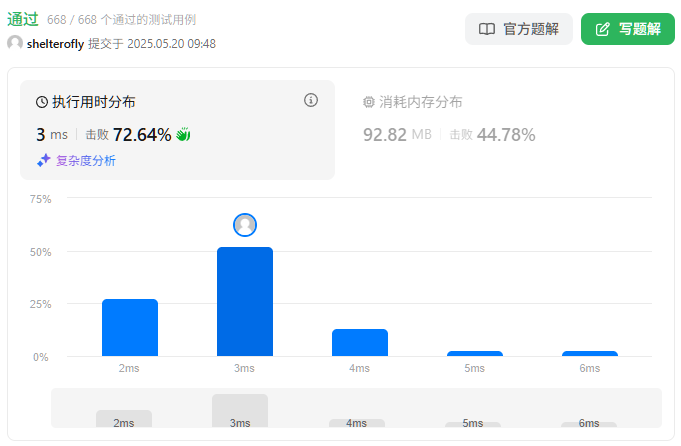
性能