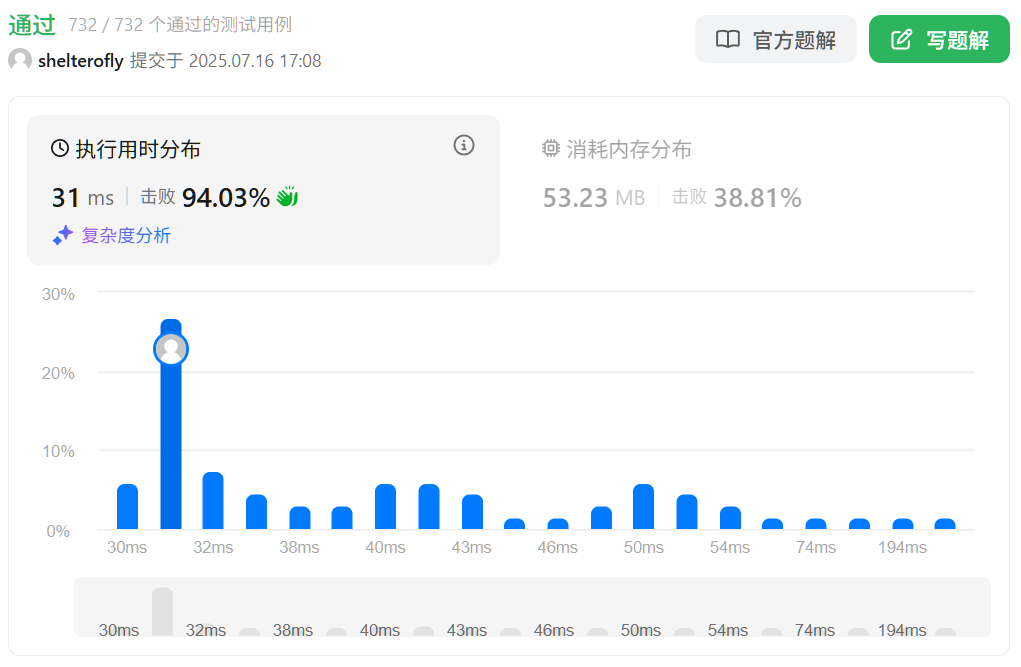
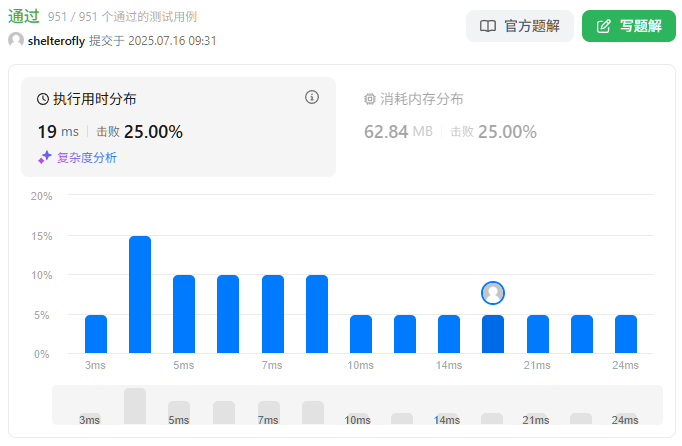
目标
你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
- 你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
- 你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
- 一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。
示例 1:
输入:fruits = [1,2,1]
输出:3
解释:可以采摘全部 3 棵树。示例 2:
输入:fruits = [0,1,2,2]
输出:3
解释:可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘,则只能采摘 [0,1] 这两棵树。示例 3:
输入:fruits = [1,2,3,2,2]
输出:4
解释:可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘,则只能采摘 [1,2] 这两棵树。示例 4:
输入:fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出:5
解释:可以采摘 [1,2,1,1,2] 这五棵树。说明:
- 1 <= fruits.length <= 10^5
- 0 <= fruits[i] < fruits.length
思路
求满足条件的子数组的最大长度,要求子数组最多包含两个不同的元素。
滑动窗口。
代码
/**
* @date 2025-08-04 8:51
*/
public class TotalFruit904 {
public int totalFruit(int[] fruits) {
int n = fruits.length;
int res = 0;
Map<Integer, Integer> map = new HashMap<>();
int l = 0;
for (int i = 0; i < n; i++) {
map.merge(fruits[i], 1, Integer::sum);
while (map.size() > 2) {
map.merge(fruits[l], -1, Integer::sum);
if (map.get(fruits[l]) == 0) {
map.remove(fruits[l]);
}
l++;
}
res = Math.max(res, i - l + 1);
}
return res;
}
}
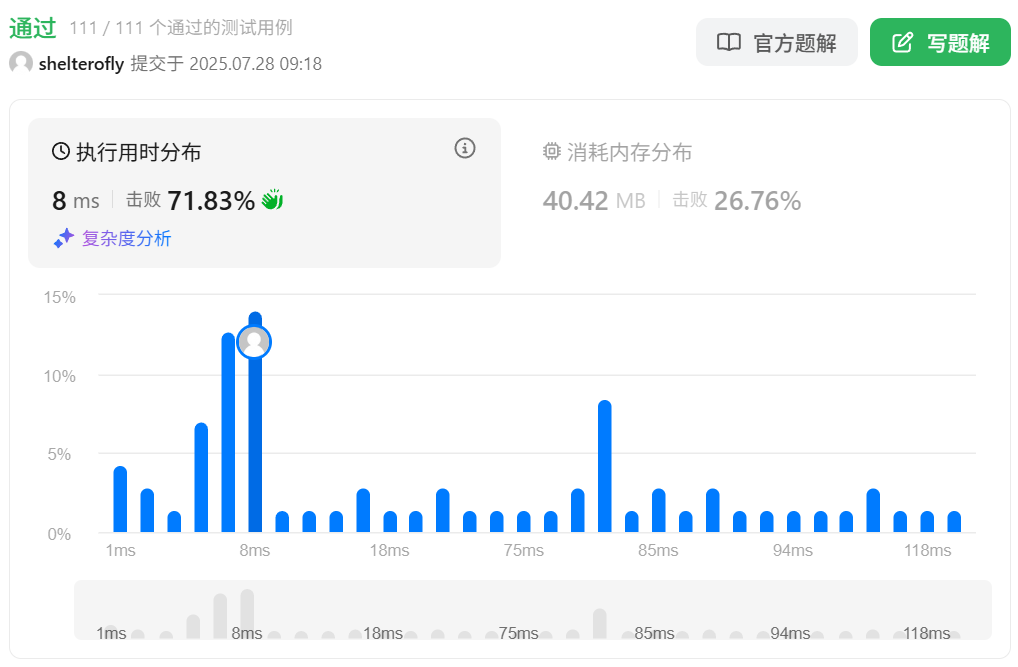
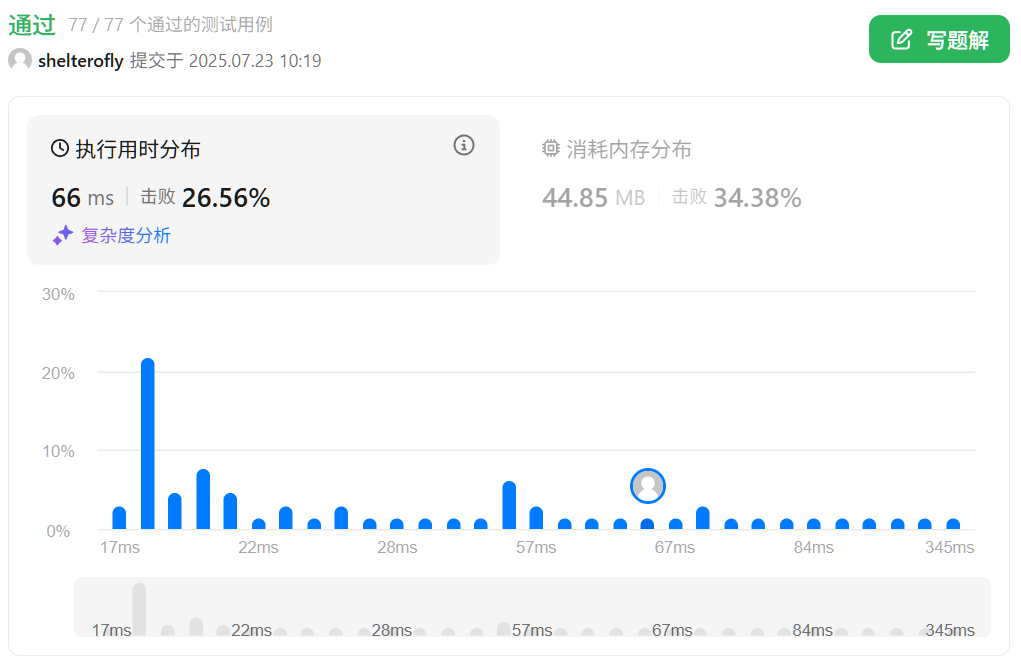
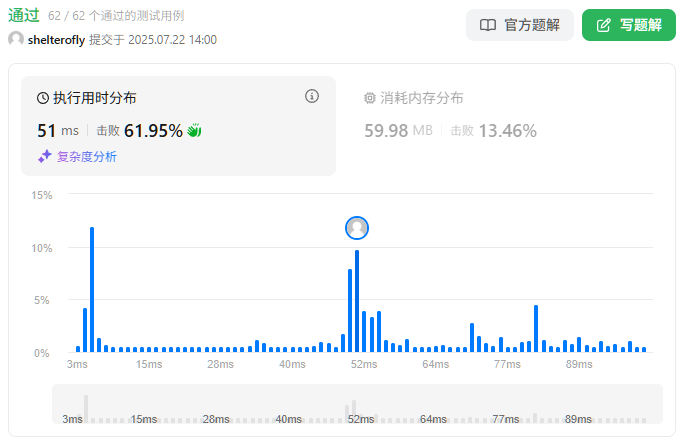
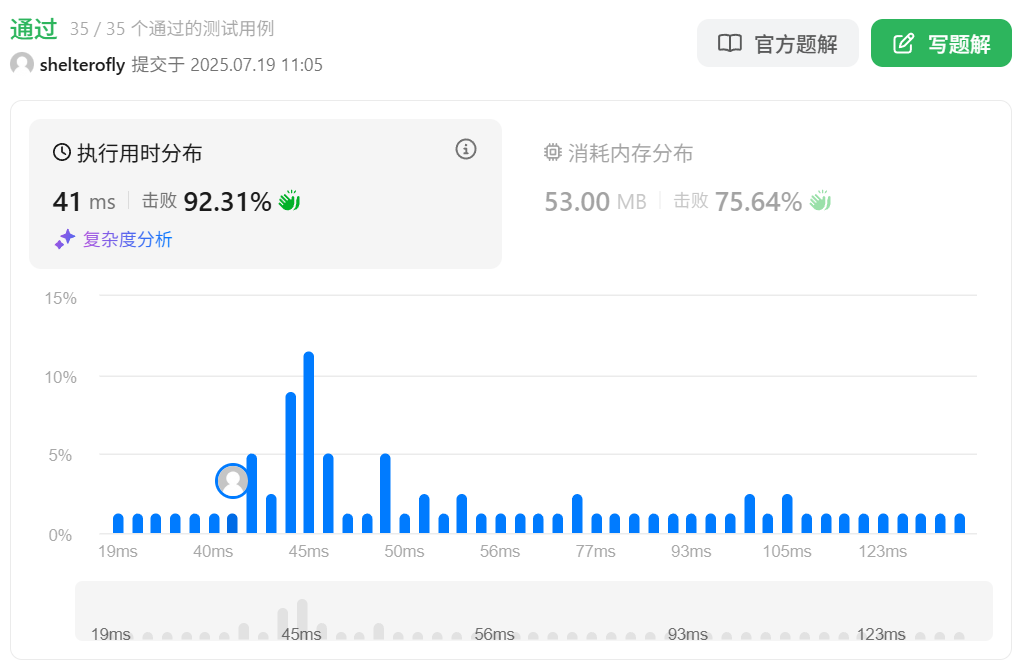
性能