目标
给你一个 events 数组,其中 events[i] = [startDayi, endDayi, valuei] ,表示第 i 个会议在 startDayi 天开始,第 endDayi 天结束,如果你参加这个会议,你能得到价值 valuei 。同时给你一个整数 k 表示你能参加的最多会议数目。
你同一时间只能参加一个会议。如果你选择参加某个会议,那么你必须 完整 地参加完这个会议。会议结束日期是包含在会议内的,也就是说你不能同时参加一个开始日期与另一个结束日期相同的两个会议。
请你返回能得到的会议价值 最大和 。
示例 1:
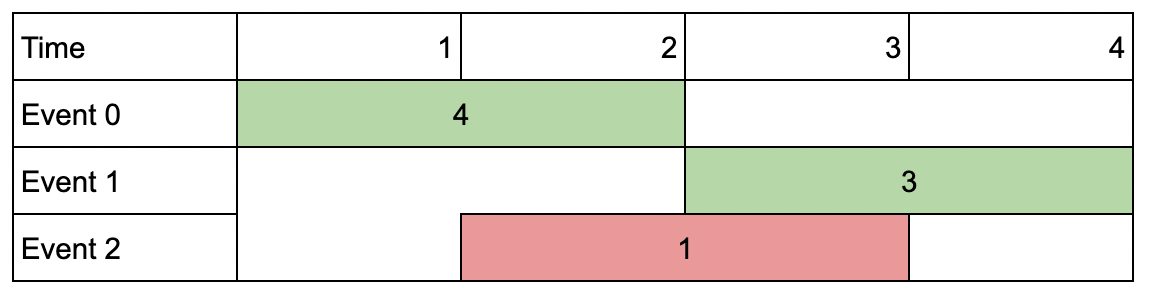
输入:events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
输出:7
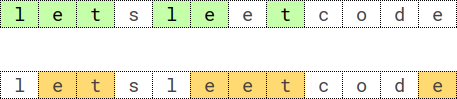
解释:选择绿色的活动会议 0 和 1,得到总价值和为 4 + 3 = 7 。示例 2:
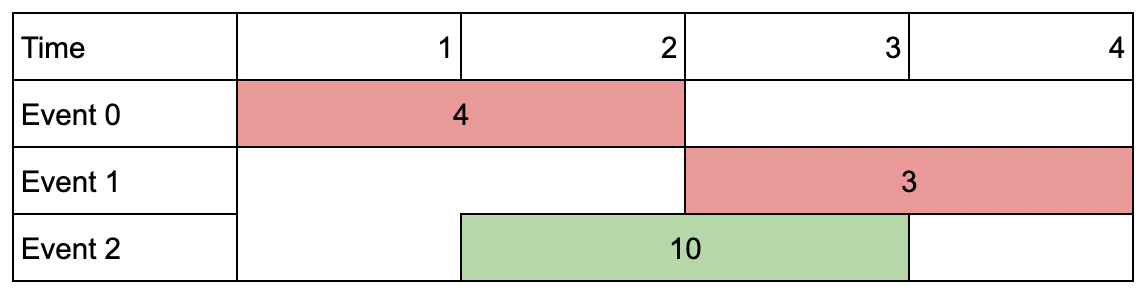
输入:events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
输出:10
解释:参加会议 2 ,得到价值和为 10 。
你没法再参加别的会议了,因为跟会议 2 有重叠。你 不 需要参加满 k 个会议。示例 3:
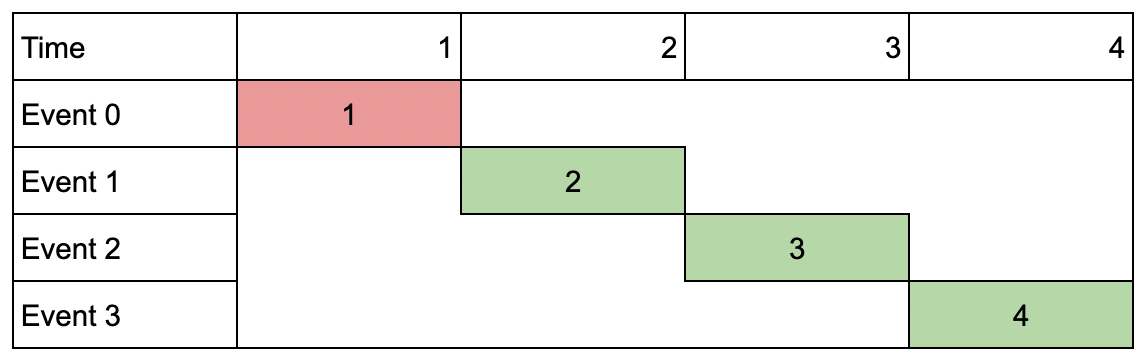
输入:events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
输出:9
解释:尽管会议互不重叠,你只能参加 3 个会议,所以选择价值最大的 3 个会议。说明:
- 1 <= k <= events.length
- 1 <= k * events.length <= 10^6
- 1 <= startDayi <= endDayi <= 10^9
- 1 <= valuei <= 10^6
思路
从 n 个会议中选择 k 个日期不冲突的参加,求参加会议的最大价值之和。
与 1353.最多可以参加的会议数目 不同之处在于必须从头到尾全程参会,并且最多参加 k 个。
定义 dp[i][k] 表示前 i - 1 个会议至多参加 k 个所能获得的最大价值。i == 0 表示没有参加任何会议。
按照结束时间排序,如果选择当前会议,则需要找到最后一个结束时间小于当前开始时间的下标 j,可以使用二分查找。
代码
/**
* @date 2025-07-08 8:47
*/
public class MaxValue1751 {
public int maxValue(int[][] events, int k) {
Arrays.sort(events, (a, b) -> a[1] - b[1]);
int n = events.length;
int[][] dp = new int[n + 1][k + 1];
for (int i = 0; i < n; i++) {
int prev = find(events, events[i][0]);
for (int j = 1; j <= k; j++) {
dp[i + 1][j] = Math.max(dp[i][j], dp[prev + 1][j - 1] + events[i][2]);
}
}
return dp[n][k];
}
public int find(int[][] events, int target) {
int r = events.length - 1;
int l = 0;
int mid = l + (r - l) / 2;
while (l <= r) {
if (events[mid][1] < target) {
l = mid + 1;
} else {
r = mid - 1;
}
mid = l + (r - l) / 2;
}
return r;
}
}
性能