目标
给你一个下标从 0 开始的二维整数数组 dimensions。
对于所有下标 i (0 <= i < dimensions.length),dimensions[i][0] 表示矩形 i 的长度,而 dimensions[i][1] 表示矩形 i 的宽度。
返回对角线最 长 的矩形的 面积 。如果存在多个对角线长度相同的矩形,返回面积最 大 的矩形的面积。
示例 1:
输入:dimensions = [[9,3],[8,6]]
输出:48
解释:
下标 = 0,长度 = 9,宽度 = 3。对角线长度 = sqrt(9 * 9 + 3 * 3) = sqrt(90) ≈ 9.487。
下标 = 1,长度 = 8,宽度 = 6。对角线长度 = sqrt(8 * 8 + 6 * 6) = sqrt(100) = 10。
因此,下标为 1 的矩形对角线更长,所以返回面积 = 8 * 6 = 48。示例 2:
输入:dimensions = [[3,4],[4,3]]
输出:12
解释:两个矩形的对角线长度相同,为 5,所以最大面积 = 12。说明:
- 1 <= dimensions.length <= 100
- dimensions[i].length == 2
- 1 <= dimensions[i][0], dimensions[i][1] <= 100
思路
依题意模拟即可。
代码
/**
* @date 2025-08-26 8:45
*/
public class AreaOfMaxDiagonal3000 {
/**
* 网友题解
*/
class Solution {
public int areaOfMaxDiagonal(int[][] dimensions) {
int ans = 0, maxL = 0;
for (int[] d : dimensions) {
int x = d[0], y = d[1];
int l = x * x + y * y;
if (l > maxL || l == maxL && x * y > ans) {
maxL = l;
ans = x * y;
}
}
return ans;
}
}
/**
* 执行通过
*/
public int areaOfMaxDiagonal(int[][] dimensions) {
int res = 0;
int diagonal = 0;
for (int[] dimension : dimensions) {
int length = dimension[0];
int width = dimension[1];
int cur = length * length + width * width;
if (diagonal < cur) {
res = length * width;
// 出错点:不要忘记更新 diagonal
diagonal = cur;
} else if (diagonal == cur) {
// 出错点:对角线相等需要分开处理,取面积的最大值
res = Math.max(res, length * width);
}
}
return res;
}
}
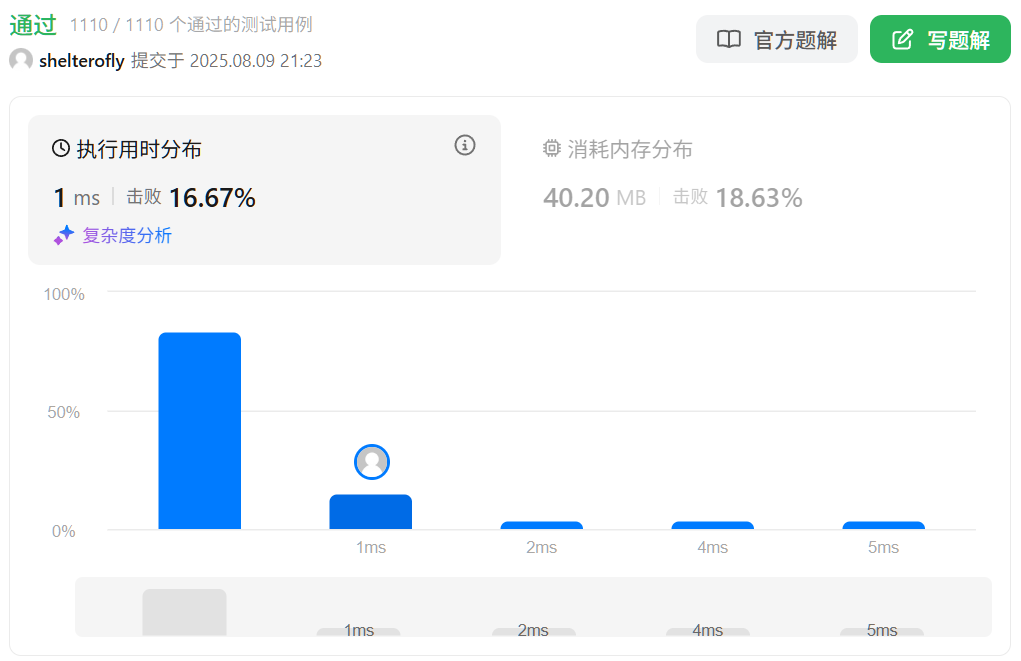
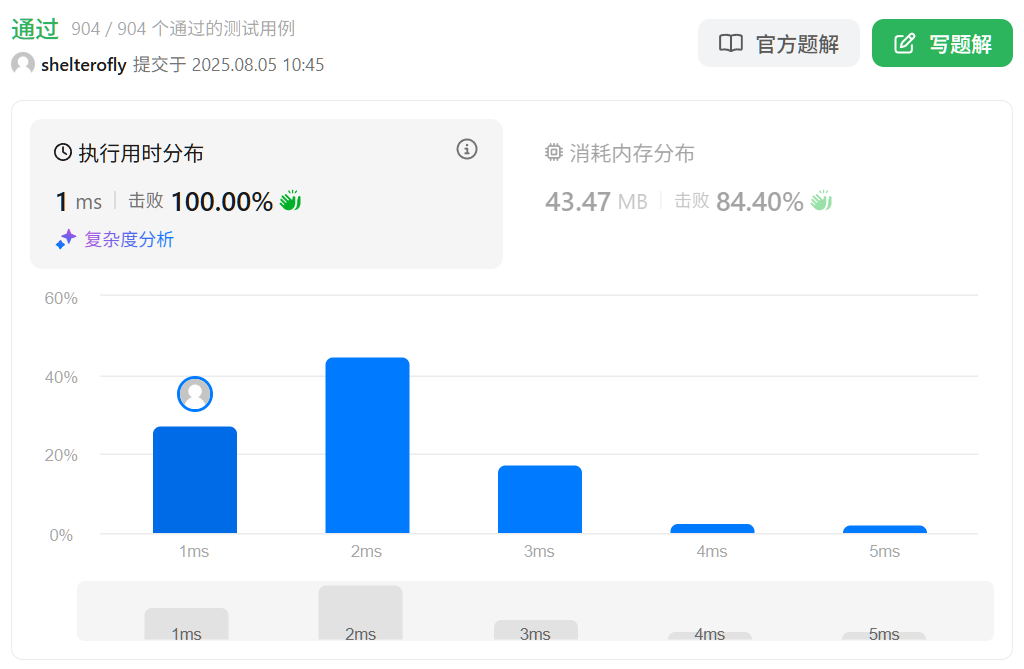
性能