标签： easy

目标

给你一个整数数组 nums 。一次操作中，你可以将 nums 中的 任意 一个元素增加或者减少 1 。

请你返回将 nums 中所有元素都可以被 3 整除的 最少 操作次数。

示例 1：

输入：nums = [1,2,3,4]
输出：3
解释：
通过以下 3 个操作，数组中的所有元素都可以被 3 整除：
将 1 减少 1 。
将 2 增加 1 。
将 4 减少 1 。

示例 2：

输入：nums = [3,6,9]
输出：0

说明：

1 <= nums.length <= 50
1 <= nums[i] <= 50

思路

统计数组中不能被 3 整除的元素个数。

代码

/**
 * @date 2025-11-22 2:02
 */
public class MinimumOperations3190 {

    public int minimumOperations(int[] nums) {
        int res = 0;
        for (int num : nums) {
            if (num % 3 != 0){
                res++;
            }
        }
        return res;
    }
}

性能

目标

给你一个整数数组 nums ，另给你一个整数 original ，这是需要在 nums 中搜索的第一个数字。

接下来，你需要按下述步骤操作：

1. 如果在 nums 中找到 original ，将 original 乘以 2 ，得到新 original（即，令 original = 2 * original）。
2. 否则，停止这一过程。
3. 只要能在数组中找到新 original ，就对新 original 继续 重复 这一过程。

返回 original 的 最终 值。

示例 1：

输入：nums = [5,3,6,1,12], original = 3
输出：24
解释： 
- 3 能在 nums 中找到。3 * 2 = 6 。
- 6 能在 nums 中找到。6 * 2 = 12 。
- 12 能在 nums 中找到。12 * 2 = 24 。
- 24 不能在 nums 中找到。因此，返回 24 。

示例 2：

输入：nums = [2,7,9], original = 4
输出：4
解释：
- 4 不能在 nums 中找到。因此，返回 4 。

说明：

• 1 <= nums.length <= 1000
• 1 <= nums[i], original <= 1000

思路

有一个数组 nums 和一个整数 original，如果数组中存在 original，可以执行操作将 original 变为 2 * original，重复执行直到无法继续为止，返回 original 的最终值。

需要反复地判断 original 是否在数组中，可以将数组放入哈希表，然后从小到大模拟操作过程。

代码

/**
 * @date 2025-11-19 8:46
 */
public class FindFinalValue2154 {

    public int findFinalValue(int[] nums, int original) {
        Set<Integer> set = new HashSet<>();
        for (int num : nums) {
            set.add(num);
        }
        while (true) {
            if (set.contains(original)) {
                original *= 2;
            } else {
                return original;
            }
        }
    }

}

性能

目标

有两种特殊字符：

• 第一种字符可以用一比特 0 表示
• 第二种字符可以用两比特（10 或 11）表示

给你一个以 0 结尾的二进制数组 bits ，如果最后一个字符必须是一个一比特字符，则返回 true 。

示例 1:

输入: bits = [1, 0, 0]
输出: true
解释: 唯一的解码方式是将其解析为一个两比特字符和一个一比特字符。
所以最后一个字符是一比特字符。

示例 2:

输入：bits = [1,1,1,0]
输出：false
解释：唯一的解码方式是将其解析为两比特字符和两比特字符。
所以最后一个字符不是一比特字符。

说明:

• 1 <= bits.length <= 1000
• bits[i] 为 0 或 1

思路

有一个二进制数组 bits 最后一个元素是 0，其中 10、11 表示一个 2 比特字符， 0 表示一个 1 比特字符，判断二进制数组的最后一个 0 是否只能解码为 1 比特字符。

实际上就是判断将数组最后一个 0 去掉之后能否解码。由于 0 可以单独解码，遇到 1 一定要与后面一个元素结合。按照这个策略，只需判断是否剩下倒数第二个元素待解码且该元素是 1。

代码

/**
 * @date 2025-11-18 8:55
 */
public class IsOneBitCharacter717 {

    public boolean isOneBitCharacter(int[] bits) {
        int n = bits.length;
        int i = 0;
        while (i < n - 1) {
            if (bits[i] == 0) {
                i++;
            } else if (i == n - 2) {
                return false;
            } else {
                i += 2;
            }
        }
        return true;
    }
}

性能

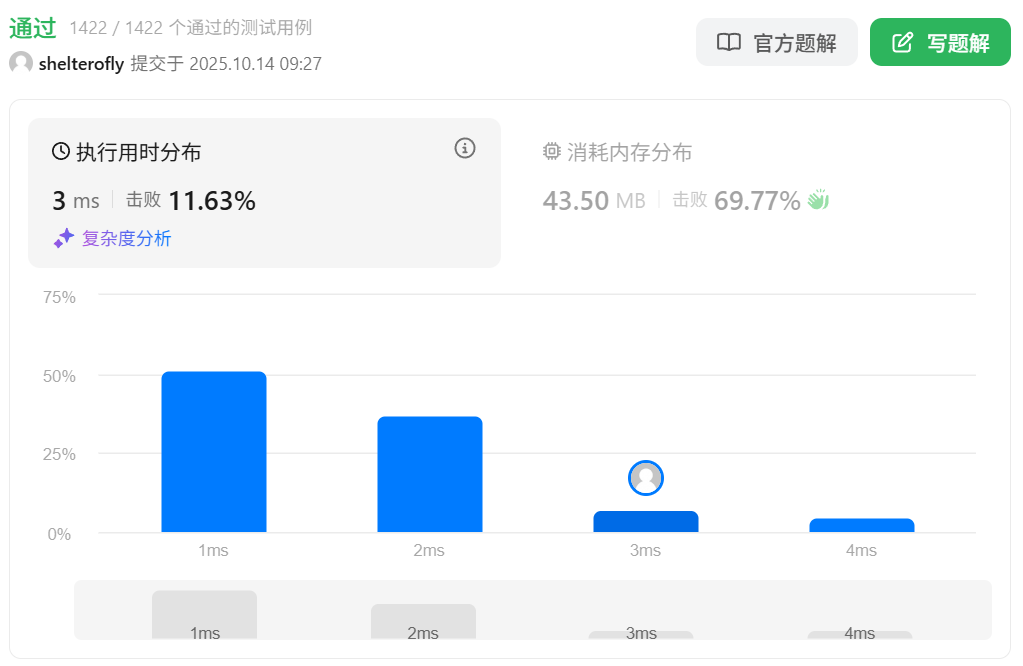
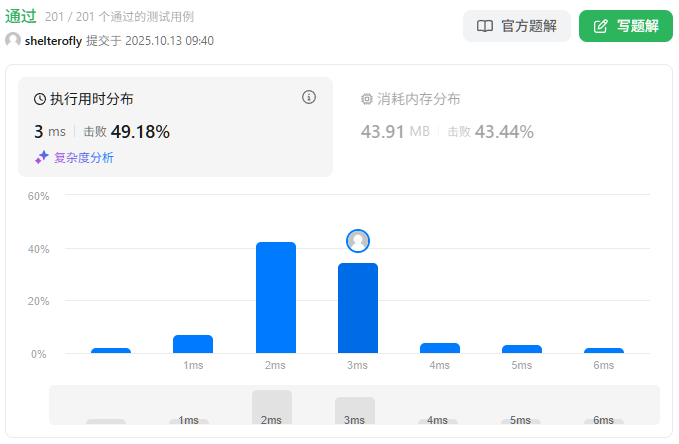
目标

给你两个 非负 整数 num1 和 num2 。

每一步 操作 中，如果 num1 >= num2 ，你必须用 num1 减 num2 ；否则，你必须用 num2 减 num1 。

• 例如，num1 = 5 且 num2 = 4 ，应该用 num1 减 num2 ，因此，得到 num1 = 1 和 num2 = 4 。然而，如果 num1 = 4且 num2 = 5 ，一步操作后，得到 num1 = 4 和 num2 = 1 。

返回使 num1 = 0 或 num2 = 0 的 操作数 。

示例 1：

输入：num1 = 2, num2 = 3
输出：3
解释：
- 操作 1 ：num1 = 2 ，num2 = 3 。由于 num1 < num2 ，num2 减 num1 得到 num1 = 2 ，num2 = 3 - 2 = 1 。
- 操作 2 ：num1 = 2 ，num2 = 1 。由于 num1 > num2 ，num1 减 num2 。
- 操作 3 ：num1 = 1 ，num2 = 1 。由于 num1 == num2 ，num1 减 num2 。
此时 num1 = 0 ，num2 = 1 。由于 num1 == 0 ，不需要再执行任何操作。
所以总操作数是 3 。

示例 2：

输入：num1 = 10, num2 = 10
输出：1
解释：
- 操作 1 ：num1 = 10 ，num2 = 10 。由于 num1 == num2 ，num1 减 num2 得到 num1 = 10 - 10 = 0 。
此时 num1 = 0 ，num2 = 10 。由于 num1 == 0 ，不需要再执行任何操作。
所以总操作数是 1 。

说明：

• 0 <= num1, num2 <= 10^5

思路

两个非负整数 num1 和 num2，如果 num1 >= num2，num1 -= num2，否则 num2 -= num1，直到 num1 或 num2 变为 0。

依题意模拟即可。

代码

/**
 * @date 2025-11-09 23:53
 */
public class CountOperations2169 {

    public int countOperations(int num1, int num2) {
        int res = 0;
        while (num1 != 0 && num2 != 0) {
            if (num1 >= num2) {
                num1 -= num2;
            } else {
                num2 -= num1;
            }
            res++;
        }
        return res;
    }
}

性能

目标

给你一个由 n 个整数组成的数组 nums，以及两个整数 k 和 x。

数组的 x-sum 计算按照以下步骤进行：

• 统计数组中所有元素的出现次数。
• 仅保留出现次数最多的前 x 个元素的每次出现。如果两个元素的出现次数相同，则数值 较大 的元素被认为出现次数更多。
• 计算结果数组的和。

注意，如果数组中的不同元素少于 x 个，则其 x-sum 是数组的元素总和。

返回一个长度为 n - k + 1 的整数数组 answer，其中 answer[i] 是 子数组 nums[i..i + k - 1] 的 x-sum。

子数组 是数组内的一个连续 非空 的元素序列。

示例 1：

输入：nums = [1,1,2,2,3,4,2,3], k = 6, x = 2
输出：[6,10,12]
解释：
对于子数组 [1, 1, 2, 2, 3, 4]，只保留元素 1 和 2。因此，answer[0] = 1 + 1 + 2 + 2。
对于子数组 [1, 2, 2, 3, 4, 2]，只保留元素 2 和 4。因此，answer[1] = 2 + 2 + 2 + 4。注意 4 被保留是因为其数值大于出现其他出现次数相同的元素（3 和 1）。
对于子数组 [2, 2, 3, 4, 2, 3]，只保留元素 2 和 3。因此，answer[2] = 2 + 2 + 2 + 3 + 3。

示例 2：

输入：nums = [3,8,7,8,7,5], k = 2, x = 2
输出：[11,15,15,15,12]
解释：
由于 k == x，answer[i] 等于子数组 nums[i..i + k - 1] 的总和。

说明：

• 1 <= n == nums.length <= 50
• 1 <= nums[i] <= 50
• 1 <= x <= k <= nums.length

思路

计算长度为 k 的滑动窗口内的 x-sum，即出现次数最大的前 x 个元素的元素和。

暴力解法是直接模拟，使用哈希表记录 元素值与出现次数，使用优先队列保存，取出现次数前 x 大的所有元素和。

代码

/**
 * @date 2025-11-04 0:27
 */
public class FindXSum3318 {

    public int[] findXSum(int[] nums, int k, int x) {
        int n = nums.length;
        int[] res = new int[n - k + 1];
        for (int i = 0; i < n - k + 1; i++) {
            Map<Integer, Counter> map = new HashMap<>();
            PriorityQueue<Counter> q = new PriorityQueue<>((a, b) -> {
                int compare = b.cnt - a.cnt;
                if (compare != 0) {
                    return compare;
                }
                return b.digit - a.digit;
            });
            for (int j = i; j < i + k; j++) {
                map.putIfAbsent(nums[j], new Counter(nums[j], 0));
                map.get(nums[j]).cnt++;
            }
            for (Counter value : map.values()) {
                q.offer(value);
            }
            int c = x;
            while (c > 0 && !q.isEmpty()) {
                Counter counter = q.poll();
                res[i] += counter.cnt * counter.digit;
                c--;
            }
        }
        return res;
    }

    public class Counter {
        int digit;
        int cnt;

        public Counter(int digit, int cnt) {
            this.digit = digit;
            this.cnt = cnt;
        }

        public Counter() {
        }
    }

}

性能

目标

数字小镇 Digitville 中，存在一个数字列表 nums，其中包含从 0 到 n - 1 的整数。每个数字本应 只出现一次，然而，有 两个 顽皮的数字额外多出现了一次，使得列表变得比正常情况下更长。

为了恢复 Digitville 的和平，作为小镇中的名侦探，请你找出这两个顽皮的数字。

返回一个长度为 2 的数组，包含这两个数字（顺序任意）。

示例 1：

输入： nums = [0,1,1,0]
输出： [0,1]
解释：
数字 0 和 1 分别在数组中出现了两次。

示例 2：

输入： nums = [0,3,2,1,3,2]
输出： [2,3]
解释:
数字 2 和 3 分别在数组中出现了两次。

示例 3：

输入： nums = [7,1,5,4,3,4,6,0,9,5,8,2]
输出： [4,5]
解释:
数字 4 和 5 分别在数组中出现了两次。

说明：

• 2 <= n <= 100
• nums.length == n + 2
• 0 <= nums[i] < n
• 输入保证 nums 中 恰好 包含两个重复的元素。

思路

长度为 n + 2 的数组，其元素由 0 1 2 …… n - 1 n 个数字以及该范围内的两个任意数字组成，找出这两个重复数字。

简单的做法是对每个元素计数，找出出现次数为 2 的元素。但是空间复杂度为 O(n)。

进阶的做法是使用位运算得到这两个重复数字的异或值，这两个数字至少有一个 bit 位不同，根据该 bit 位分组，最终得到这两个数字。

代码

/**
 * @date 2025-10-31 9:05
 */
public class GetSneakyNumbers3289 {

    public int[] getSneakyNumbers(int[] nums) {
        int n = nums.length;
        int[] cnt = new int[n];
        List<Integer> list = new ArrayList<>();
        for (int num : nums) {
            cnt[num]++;
            if (cnt[num] == 2){
                list.add(num);
            }
        }
        int[] res = new int[2];
        for (int i = 0; i < 2; i++) {
            res[i] = list.get(i);
        }
        return res;
    }
}

性能

目标

给你一个正整数 n。

返回 大于等于 n 且二进制表示仅包含 置位 位的 最小 整数 x 。

置位 位指的是二进制表示中值为 1 的位。

示例 1：

输入： n = 5
输出： 7
解释：
7 的二进制表示是 "111"。

示例 2：

输入： n = 10
输出： 15
解释：
15 的二进制表示是 "1111"。

示例 3：

输入： n = 3
输出： 3
解释：
3 的二进制表示是 "11"。

说明：

• 1 <= n <= 1000

思路

返回大于等于 n 并且所有 bit 位均为 1 的最小整数。

代码

/**
 * @date 2025-10-29 8:40
 */
public class SmallestNumber3370 {

    public int smallestNumber(int n) {
        int l = 32 - Integer.numberOfLeadingZeros(n);
        return (1 << l) - 1;
    }

}

性能

目标

给你一个整数数组 nums 。

开始时，选择一个满足 nums[curr] == 0 的起始位置 curr ，并选择一个移动 方向 ：向左或者向右。

此后，你需要重复下面的过程：

• 如果 curr 超过范围 [0, n - 1] ，过程结束。
• 如果 nums[curr] == 0 ，沿当前方向继续移动：如果向右移，则 递增 curr ；如果向左移，则 递减 curr 。
• 如果 nums[curr] > 0:
  • 将 nums[curr] 减 1 。
  • 反转 移动方向（向左变向右，反之亦然）。
  • 沿新方向移动一步。

如果在结束整个过程后，nums 中的所有元素都变为 0 ，则认为选出的初始位置和移动方向 有效 。

返回可能的有效选择方案数目。

示例 1：

输入：nums = [1,0,2,0,3]
输出：2
解释：
可能的有效选择方案如下：
选择 curr = 3 并向左移动。
[1,0,2,0,3] -> [1,0,2,0,3] -> [1,0,1,0,3] -> [1,0,1,0,3] -> [1,0,1,0,2] -> [1,0,1,0,2] -> [1,0,0,0,2] -> [1,0,0,0,2] -> [1,0,0,0,1] -> [1,0,0,0,1] -> [1,0,0,0,1] -> [1,0,0,0,1] -> [0,0,0,0,1] -> [0,0,0,0,1] -> [0,0,0,0,1] -> [0,0,0,0,1] -> [0,0,0,0,0].
选择 curr = 3 并向右移动。
[1,0,2,0,3] -> [1,0,2,0,3] -> [1,0,2,0,2] -> [1,0,2,0,2] -> [1,0,1,0,2] -> [1,0,1,0,2] -> [1,0,1,0,1] -> [1,0,1,0,1] -> [1,0,0,0,1] -> [1,0,0,0,1] -> [1,0,0,0,0] -> [1,0,0,0,0] -> [1,0,0,0,0] -> [1,0,0,0,0] -> [0,0,0,0,0].

示例 2：

输入：nums = [2,3,4,0,4,1,0]
输出：0
解释：
不存在有效的选择方案。

说明：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 100
• 至少存在一个元素 i 满足 nums[i] == 0 。

思路

有一个数组 nums，选一个元素值为 0 的位置作为起点，然后选择向左或向右移动，每遇到一个不为 0 的位置，将其元素值减一并沿相反方向继续移动，直到超出数组下标范围。求有多少种方案（由起点位置和初始移动方向唯一确定一个方案）可以使数组所有元素最终变为 0。

计算数组的前后缀，如果左侧等于右侧，可以选两个方向，如果左右两侧相差 1，可以选一个方向。

代码

/**
 * @date 2025-10-28 8:49
 */
public class CountValidSelections3354 {

    public int countValidSelections(int[] nums) {
        int n = nums.length;
        int[] prefix = new int[n + 1];
        int[] suffix = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            prefix[i] = prefix[i - 1] + nums[i - 1];
            suffix[n - i] = suffix[n - i + 1] + nums[n - i];
        }
        int res = 0;
        for (int i = 0; i < n; i++) {
            if (nums[i] != 0) {
                continue;
            }
            if (prefix[i] == suffix[i + 1]) {
                res += 2;
            }
            if (prefix[i] == suffix[i + 1] + 1 || prefix[i] == suffix[i + 1] - 1) {
                res++;
            }
        }
        return res;
    }

}

性能

目标

Hercy 想要为购买第一辆车存钱。他 每天 都往力扣银行里存钱。

最开始，他在周一的时候存入 1 块钱。从周二到周日，他每天都比前一天多存入 1 块钱。在接下来每一个周一，他都会比 前一个周一 多存入 1 块钱。

给你 n ，请你返回在第 n 天结束的时候他在力扣银行总共存了多少块钱。

示例 1：

输入：n = 4
输出：10
解释：第 4 天后，总额为 1 + 2 + 3 + 4 = 10 。

示例 2：

输入：n = 10
输出：37
解释：第 10 天后，总额为 (1 + 2 + 3 + 4 + 5 + 6 + 7) + (2 + 3 + 4) = 37 。注意到第二个星期一，Hercy 存入 2 块钱。

示例 3：

输入：n = 20
输出：96
解释：第 20 天后，总额为 (1 + 2 + 3 + 4 + 5 + 6 + 7) + (2 + 3 + 4 + 5 + 6 + 7 + 8) + (3 + 4 + 5 + 6 + 7 + 8) = 96 。

说明：

• 1 <= n <= 1000

思路

week 0 28 + 7 * 0
week 1 28 + 7 * 1
week 2 28 + 7 * 2
week 3 28 + 7 * 3
...

0 ~ n - 1 周的累加和 n * 28 + (n - 1) * n / 2 * 7

week n 1 + 2 + …… + rem       + n * rem
即     (rem * (rem + 1) / 2)  + n * rem
          当前周的前rem项和

代码

/**
 * @date 2025-10-25 22:11
 */
public class TotalMoney1716 {

    public int totalMoney(int n) {
        int oneWeek = 28;
        int times = n / 7;
        int rem = n % 7;
        return (1 + rem) * rem / 2 + times * oneWeek + Math.max(0, (times - 1) * times / 2) * 7 + times * rem;
    }

}

性能