目标
给定一个 8 x 8 的棋盘,只有一个 白色的车,用字符 'R' 表示。棋盘上还可能存在白色的象 'B' 以及黑色的卒 'p'。空方块用字符 '.' 表示。
车可以按水平或竖直方向(上,下,左,右)移动任意个方格直到它遇到另一个棋子或棋盘的边界。如果它能够在一次移动中移动到棋子的方格,则能够 吃掉 棋子。
注意:车不能穿过其它棋子,比如象和卒。这意味着如果有其它棋子挡住了路径,车就不能够吃掉棋子。
返回白车将能 吃掉 的 卒的数量。
示例 1:

输入:
[
[".",".",".",".",".",".",".","."],
[".",".",".","p",".",".",".","."],
[".",".",".","R",".",".",".","p"],
[".",".",".",".",".",".",".","."],
[".",".",".",".",".",".",".","."],
[".",".",".","p",".",".",".","."],
[".",".",".",".",".",".",".","."],
[".",".",".",".",".",".",".","."]
]
输出:3
解释:
在本例中,车能够吃掉所有的卒。
示例 2:

输入:
[
[".",".",".",".",".",".",".","."],
[".","p","p","p","p","p",".","."],
[".","p","p","B","p","p",".","."],
[".","p","B","R","B","p",".","."],
[".","p","p","B","p","p",".","."],
[".","p","p","p","p","p",".","."],
[".",".",".",".",".",".",".","."],
[".",".",".",".",".",".",".","."]
]
输出:0
解释:
象阻止了车吃掉任何卒。
示例 3:
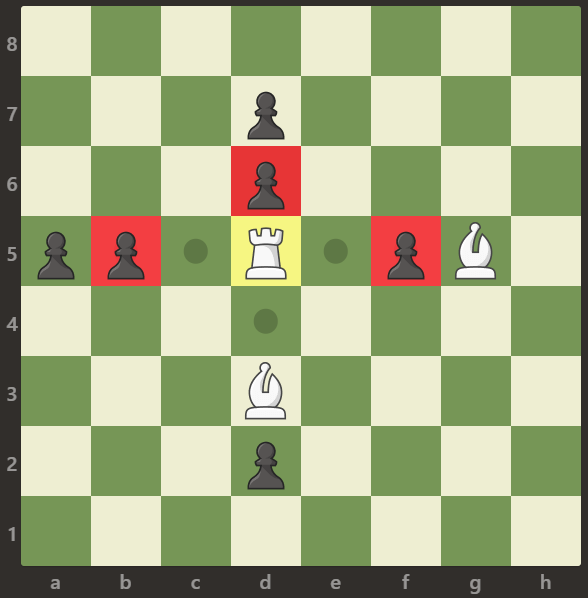
输入:
[
[".",".",".",".",".",".",".","."]
[".",".",".","p",".",".",".","."],
[".",".",".","p",".",".",".","."],
["p","p",".","R",".","p","B","."],
[".",".",".",".",".",".",".","."],
[".",".",".","B",".",".",".","."],
[".",".",".","p",".",".",".","."],
[".",".",".",".",".",".",".","."]
]
输出:3
解释:
车可以吃掉位置 b5,d6 和 f5 的卒。
说明:
- board.length == 8
- board[i].length == 8
board[i][j] 可以是 'R','.','B' 或 'p'- 只有一个格子上存在
board[i][j] == 'R'
思路
8 x 8 的棋盘上有一个白车 R,若干个白象 B 和黑卒 'p',空格由 '.' 表示。问白车能够吃掉黑卒的数量,注意车只能吃掉同行同列四个方向上第一个遇到的黑卒。
首先需要找到白车的位置,按行遍历棋盘,记录当前行上一个棋子,遇到白车时判断上一个棋子是否是黑卒,如果是计入结果,然后判断后面遇到的第一个棋子,如果是黑卒计入结果。当前行遍历完成后结束循环,按照同样方法遍历白车所在列即可。
代码
/**
* @date 2024-12-06 9:05
*/
public class NumRookCaptures999 {
public int numRookCaptures(char[][] board) {
int res = 0;
int rookRow = -1;
int rookCol = -1;
here:
for (int i = 0; i < 8; i++) {
// 首先按行遍历,找到白色车的位置(rookRow, rookCol),同时判断它前后的棋子是否是黑卒
char[] row = board[i];
char last = '.';
for (int j = 0; j < 8; j++) {
if (row[j] == 'R') {
// 如果找到白车,判断当前行前面的棋子是否是黑卒
if (last == 'p') {
res++;
}
// 记录坐标
rookCol = j;
rookRow = i;
} else if (rookCol != -1 && row[j] != '.') {
// 判断后面第一个棋子是否是黑卒
if (row[j] == 'p') {
res++;
}
break here;
}
if (row[j] != '.') {
last = row[j];
}
}
if (rookCol != -1) {
break;
}
}
for (int i = rookRow - 1; i >= 0; i--) {
if (board[i][rookCol] != '.') {
// 找到上面第一个棋子
if (board[i][rookCol] == 'p') {
res++;
}
break;
}
}
for (int i = rookRow + 1; i < 8; i++) {
if (board[i][rookCol] != '.') {
// 找到下面第一个棋子
if (board[i][rookCol] == 'p') {
res++;
}
break;
}
}
return res;
}
}
性能