目标
有一个 8 x 8 的棋盘,它包含 n 个棋子(棋子包括车,后和象三种)。给你一个长度为 n 的字符串数组 pieces ,其中 pieces[i] 表示第 i 个棋子的类型(车,后或象)。除此以外,还给你一个长度为 n 的二维整数数组 positions ,其中 positions[i] = [ri, ci] 表示第 i 个棋子现在在棋盘上的位置为 (ri, ci) ,棋盘下标从 1 开始。
棋盘上每个棋子都可以移动 至多一次 。每个棋子的移动中,首先选择移动的 方向 ,然后选择 移动的步数 ,同时你要确保移动过程中棋子不能移到棋盘以外的地方。棋子需按照以下规则移动:
- 车可以 水平或者竖直 从 (r, c) 沿着方向 (r+1, c),(r-1, c),(r, c+1) 或者 (r, c-1) 移动。
- 后可以 水平竖直或者斜对角 从 (r, c) 沿着方向 (r+1, c),(r-1, c),(r, c+1),(r, c-1),(r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1) 移动。
- 象可以 斜对角 从 (r, c) 沿着方向 (r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1) 移动。
移动组合 包含所有棋子的 移动 。每一秒,每个棋子都沿着它们选择的方向往前移动 一步 ,直到它们到达目标位置。所有棋子从时刻 0 开始移动。如果在某个时刻,两个或者更多棋子占据了同一个格子,那么这个移动组合 不有效 。
请你返回 有效 移动组合的数目。
注意:
- 初始时,不会有两个棋子 在 同一个位置。
- 有可能在一个移动组合中,有棋子不移动。
- 如果两个棋子 直接相邻 且两个棋子下一秒要互相占据对方的位置,可以将它们在同一秒内 交换位置。
示例 1:
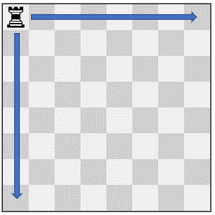
输入:pieces = ["rook"], positions = [[1,1]]
输出:15
解释:上图展示了棋子所有可能的移动。
示例 2:
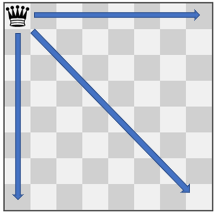
输入:pieces = ["queen"], positions = [[1,1]]
输出:22
解释:上图展示了棋子所有可能的移动。
示例 3:

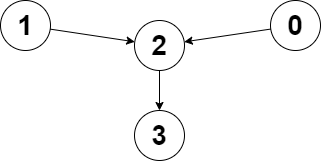
输入:pieces = ["bishop"], positions = [[4,3]]
输出:12
解释:上图展示了棋子所有可能的移动。
示例 4:

输入:pieces = ["rook","rook"], positions = [[1,1],[8,8]]
输出:223
解释:每个车有 15 种移动,所以总共有 15 * 15 = 225 种移动组合。
但是,有两个是不有效的移动组合:
- 将两个车都移动到 (8, 1) ,会导致它们在同一个格子相遇。
- 将两个车都移动到 (1, 8) ,会导致它们在同一个格子相遇。
所以,总共有 225 - 2 = 223 种有效移动组合。
注意,有两种有效的移动组合,分别是一个车在 (1, 8) ,另一个车在 (8, 1) 。
即使棋盘状态是相同的,这两个移动组合被视为不同的,因为每个棋子移动操作是不相同的。
示例 5:

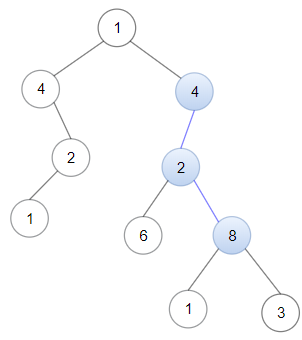
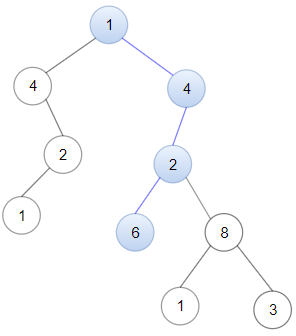
输入:pieces = ["queen","bishop"], positions = [[5,7],[3,4]]
输出:281
解释:总共有 12 * 24 = 288 种移动组合。
但是,有一些不有效的移动组合:
- 如果后停在 (6, 7) ,它会阻挡象到达 (6, 7) 或者 (7, 8) 。
- 如果后停在 (5, 6) ,它会阻挡象到达 (5, 6) ,(6, 7) 或者 (7, 8) 。
- 如果象停在 (5, 2) ,它会阻挡后到达 (5, 2) 或者 (5, 1) 。
在 288 个移动组合当中,281 个是有效的。
说明:
- n == pieces.length
- n == positions.length
- 1 <= n <= 4
- pieces 只包含字符串 "rook" ,"queen" 和 "bishop" 。
- 棋盘上最多只有一个后。
- 1 <= ri, ci <= 8
- 每一个 positions[i] 互不相同。
思路
有一个 8 x 8 的棋盘,行列编号从 1 ~ 8。棋盘上有 n 个棋子,pieces[i] 表示棋子 i 的类型,rook 表示车,queen 表示皇后,bishop 表示象,positions[i] = [ri, ci] 表示棋子 i 所在行编号为 ri,所在列编号为 ci。棋盘上的每个棋子都可以移动 至多 一步,不同的棋子移动方式不同,参考国际象棋。车走竖线或横线,象走斜线,皇后走竖线、横线或斜线,不能跳过其它棋子。
特别注意,我们求的是 有效移动 组合,重点在 移动 而不是最终状态,比如示例4。
棋盘大小固定,考虑车移动或者不移动,它最多有 15 种移动的可能,包括不移动或者移动到相应方向上的其它格子共 1 + 2 * 7 种。由于棋盘是偶数没有中间格子,所以象有 8 + 6 种。同理皇后可能的移动方式最多有 28 种,包括不移动或者移动相应方向上的其它格子 1 + 2 * 7 + 7 + 6 种,如果它位于一条 8 格的对角线上,除去自身还剩 7 格,它所在的另一对角线剩余 6 个格子。
题目描述里面非常让人迷惑的一点是既允许相邻棋子同时交换位置,而示例5又说棋子会阻挡其它棋子通行。这个题的难点在于如果按照棋盘状态去枚举的话,当两个棋子相遇的时候不知道是否应该穿越,如果穿越的话就会移动另一个棋子,如何去重?我们必须将移动的步数考虑进去,如果两个棋子相遇时都没有到达目标位置那么它们可以穿过。否则,某个棋子提前停下,另一个棋子行进到相同的位置发生碰撞,不符合题目条件。
参考题解思路写出来了。
代码
/**
* @date 2024-12-04 14:24
*/
public class CountCombinations2056 {
public static class Move {
public int x;
public int y;
public int dx;
public int dy;
public int step;
public Move(int x, int y, int dx, int dy, int step) {
this.x = x;
this.y = y;
this.dx = dx;
this.dy = dy;
this.step = step;
}
}
public int[][] rookDir = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int[][] bishopDir = new int[][]{{-1, -1}, {1, 1}, {1, -1}, {-1, 1}};
public int[][] queenDir = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}, {-1, -1}, {1, 1}, {1, -1}, {-1, 1}};
/**
* 预处理每个棋子可行的移动方案、起点、方向、步数
*/
public int countCombinations(String[] pieces, int[][] positions) {
int n = pieces.length;
Move[][] moves = new Move[n][];
for (int i = 0; i < n; i++) {
moves[i] = generateAllValidMove(pieces[i], positions[i]);
}
Move[] curMove = new Move[n];
return dfs(0, n, curMove, moves);
}
/**
* 回溯,先从棋子0中选一个可行的移动方案,然后进入下一层,
* 从棋子1中选一个可行的移动方案,判断当前方案与前面所选的移动方案是否存在某一时刻使得两个棋子占据同一个格子
* 如果不存在就进入下一层,否则枚举另一个方案。
* i 表示枚举第 i 个棋子的合法移动方案
* curMove 表示前面棋子选择的移动方案,用于下一层比较移动方案是否合法
* moves 表示所有棋子的移动方案
*/
public int dfs(int i, int n, Move[] curMove, Move[][] moves) {
if (i == n) {
return 1;
}
int cnt = 0;
here:
for (Move move : moves[i]) {
for (int j = 0; j < i; j++) {
if (!valid(move, curMove[j])) {
continue here;
}
}
curMove[i] = move;
cnt += dfs(i + 1, n, curMove, moves);
}
return cnt;
}
public boolean valid(Move move, Move curMove) {
int x1 = move.x;
int y1 = move.y;
int x2 = curMove.x;
int y2 = curMove.y;
// 步数小的会提前停下来,如果它们坐标相同说明存在在某一时刻使得两个棋子移动到同一个位置上,不合法
for (int i = 0; i < Math.max(move.step, curMove.step); i++) {
if (i < move.step) {
x1 += move.dx;
y1 += move.dy;
}
if (i < curMove.step) {
x2 += curMove.dx;
y2 += curMove.dy;
}
if (x1 == x2 && y1 == y2) {
return false;
}
}
return true;
}
/**
* 生成该棋子所有可能的移动方案
* 起点,方向,步数
*/
public Move[] generateAllValidMove(String pieces, int[] positions) {
int[][] directions = null;
switch (pieces) {
case "rook":
directions = rookDir;
break;
case "bishop":
directions = bishopDir;
break;
case "queen":
directions = queenDir;
break;
default:
}
if (directions == null) {
return null;
}
List<Move> moves = new ArrayList<>();
int x = positions[0];
int y = positions[1];
// 将不移动的情况加入集合
moves.add(new Move(x, y, 0, 0, 0));
// 遍历该棋子允许的行进方向,
for (int[] dir : directions) {
int dx = dir[0];
int dy = dir[1];
int step = 0;
x = positions[0] + dx;
y = positions[1] + dy;
while (x > 0 && x <= 8 && y > 0 && y <= 8) {
moves.add(new Move(positions[0], positions[1], dx, dy, ++step));
x += dx;
y += dy;
}
}
return moves.toArray(new Move[0]);
}
}
性能