目标
在一个由 m 个用户组成的社交网络里,我们获取到一些用户之间的好友关系。两个用户之间可以相互沟通的条件是他们都掌握同一门语言。
给你一个整数 n ,数组 languages 和数组 friendships ,它们的含义如下:
- 总共有 n 种语言,编号从 1 到 n 。
- languages[i] 是第 i 位用户掌握的语言集合。
- friendships[i] = [ui, vi] 表示 ui 和 vi 为好友关系。
你可以选择 一门 语言并教会一些用户,使得所有好友之间都可以相互沟通。请返回你 最少 需要教会多少名用户。
请注意,好友关系没有传递性,也就是说如果 x 和 y 是好友,且 y 和 z 是好友, x 和 z 不一定是好友。
示例 1:
输入:n = 2, languages = [[1],[2],[1,2]], friendships = [[1,2],[1,3],[2,3]]
输出:1
解释:你可以选择教用户 1 第二门语言,也可以选择教用户 2 第一门语言。
示例 2:
输入:n = 3, languages = [[2],[1,3],[1,2],[3]], friendships = [[1,4],[1,2],[3,4],[2,3]]
输出:2
解释:教用户 1 和用户 3 第三门语言,需要教 2 名用户。
说明:
- 2 <= n <= 500
- languages.length == m
- 1 <= m <= 500
- 1 <= languages[i].length <= n
- 1 <= languages[i][j] <= n
- 1 <= ui < vi <= languages.length
- 1 <= friendships.length <= 500
- 所有的好友关系 (ui, vi) 都是唯一的。
- languages[i] 中包含的值互不相同。
思路
有 n 种语言,编号 1 ~ n,同时有 m 个用户,编号从 1 ~ m,languages[i] 表示编号为 i + 1 的用户所掌握的语言,friendships 数组记录了用户的朋友关系。现在可以选择 一门 语言教会任意用户使得所有朋友都可以沟通,求需要教的最少人数。
找出无法沟通的朋友关系(统计总人数 total),统计每一种语言的人数 cnt[i](注意去重),最少人数即 total - max(cnt)。
代码
/**
* @date 2025-09-10 8:49
*/
public class MinimumTeachings1733 {
public int minimumTeachings(int n, int[][] languages, int[][] friendships) {
int m = languages.length;
int[] cnt = new int[n + 1];
HashSet<Integer>[] lang = new HashSet[m + 1];
Arrays.setAll(lang, x -> new HashSet<>());
for (int i = 0; i < m; i++) {
for (int language : languages[i]) {
lang[i + 1].add(language);
}
}
Set<Integer> set = new HashSet<>();
for (int[] friendship : friendships) {
int a = friendship[0];
int b = friendship[1];
HashSet<Integer> tmp = new HashSet<>(lang[a]);
tmp.retainAll(lang[b]);
if (tmp.size() == 0) {
if (!set.contains(a)) {
for (Integer t : lang[a]) {
cnt[t]++;
}
set.add(a);
}
if (!set.contains(b)) {
for (Integer t : lang[b]) {
cnt[t]++;
}
set.add(b);
}
}
}
return set.size() - Arrays.stream(cnt).max().orElse(0);
}
}
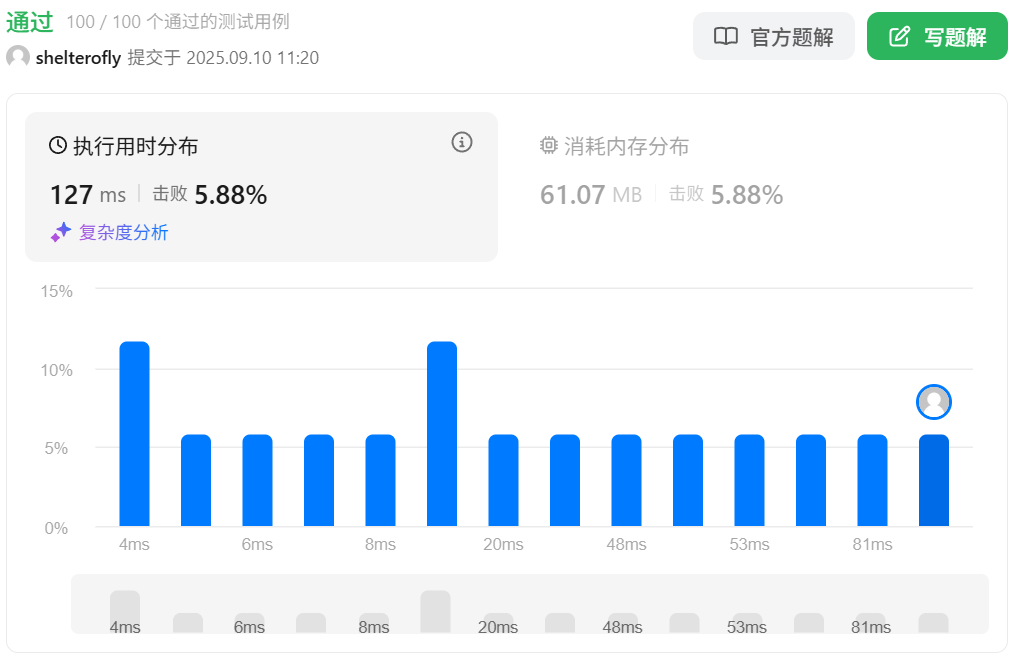
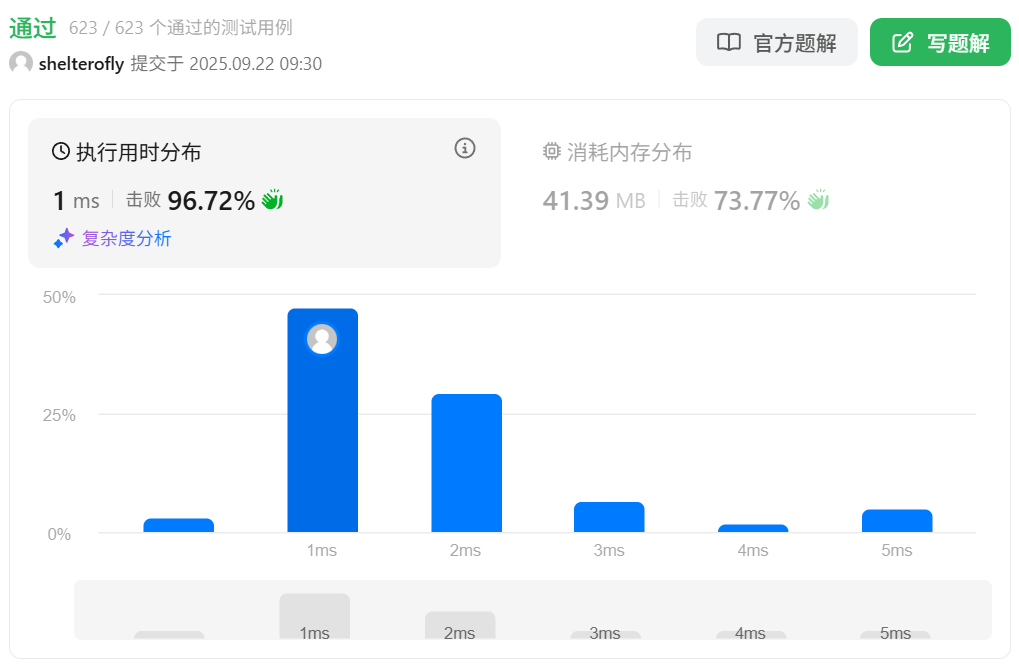
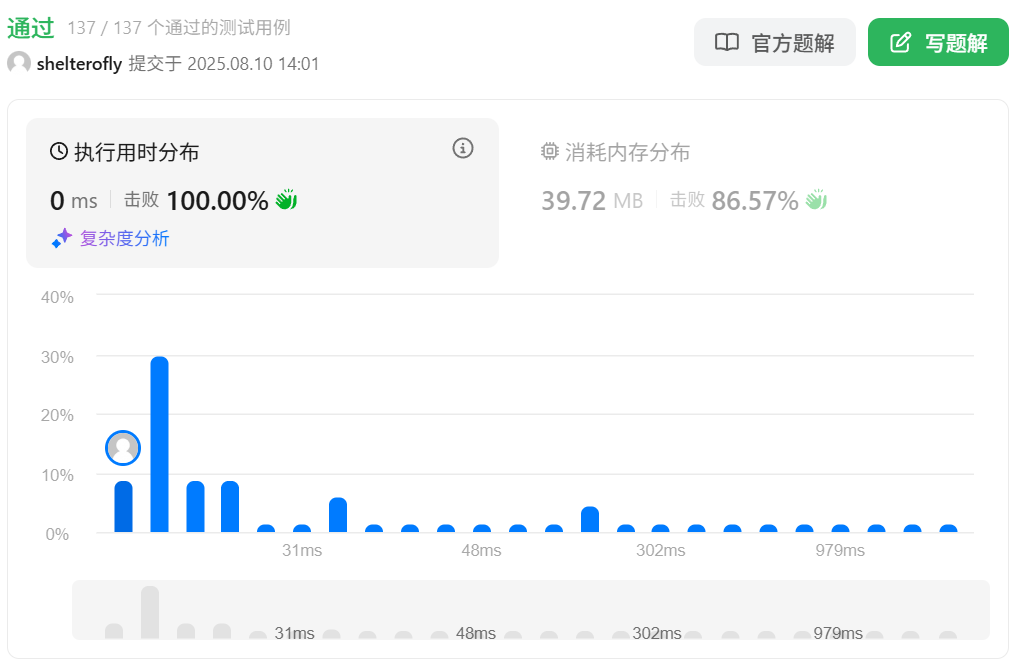
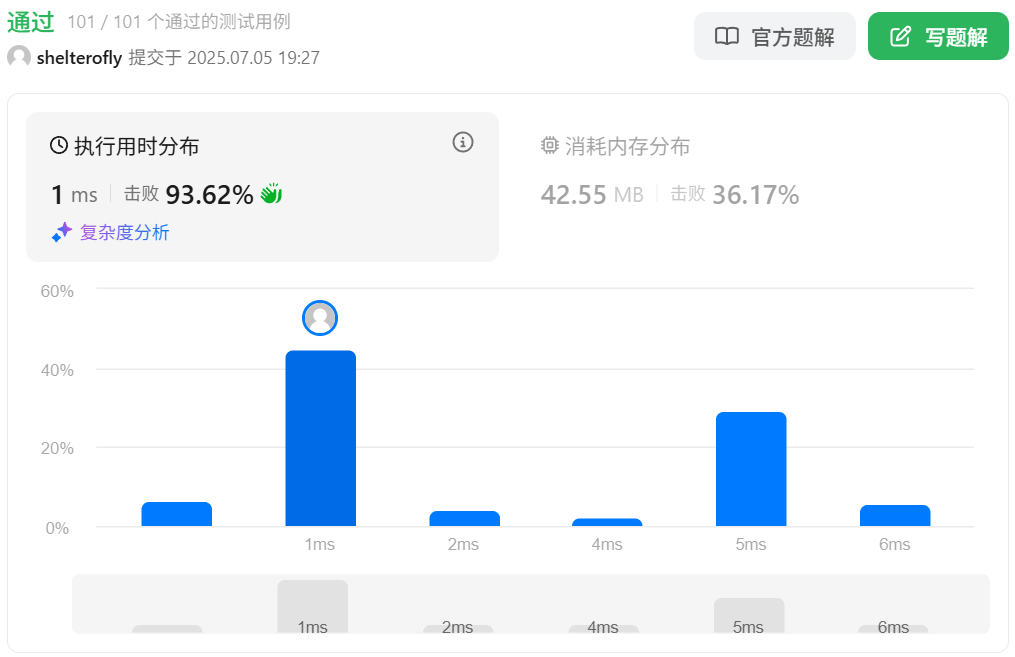
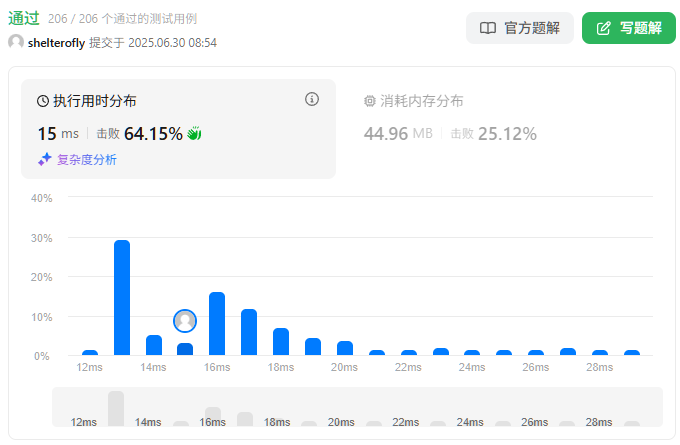
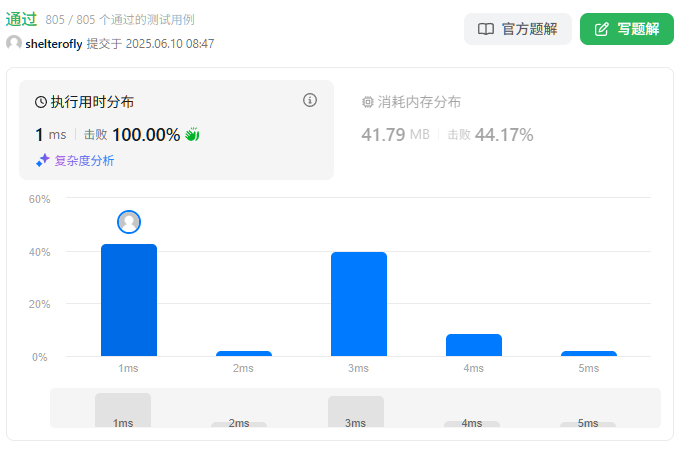
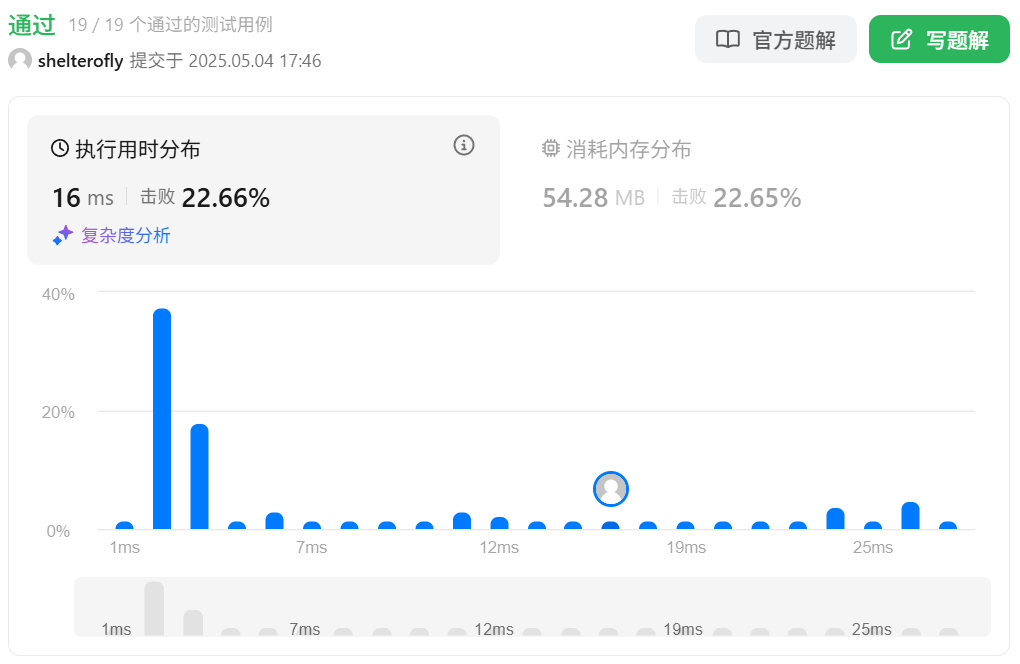
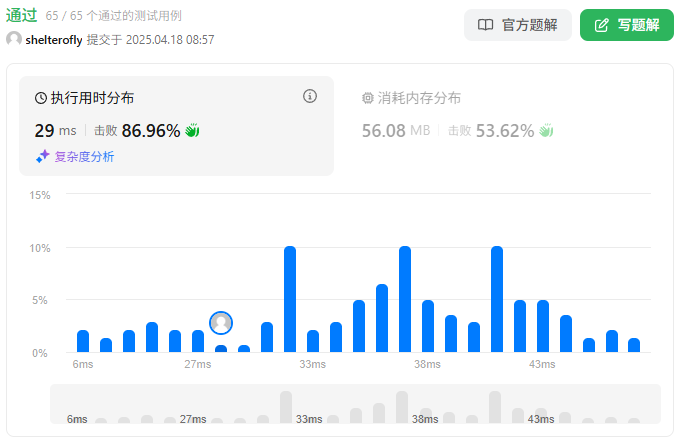
性能