目标
给你一个整数 n 表示一棵 满二叉树 里面节点的数目,节点编号从 1 到 n 。根节点编号为 1 ,树中每个非叶子节点 i 都有两个孩子,分别是左孩子 2 i 和右孩子 2 i + 1 。
树中每个节点都有一个值,用下标从 0 开始、长度为 n 的整数数组 cost 表示,其中 cost[i] 是第 i + 1 个节点的值。每次操作,你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。
你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。
注意:
- 满二叉树 指的是一棵树,它满足树中除了叶子节点外每个节点都恰好有 2 个子节点,且所有叶子节点距离根节点距离相同。
- 路径值 指的是路径上所有节点的值之和。
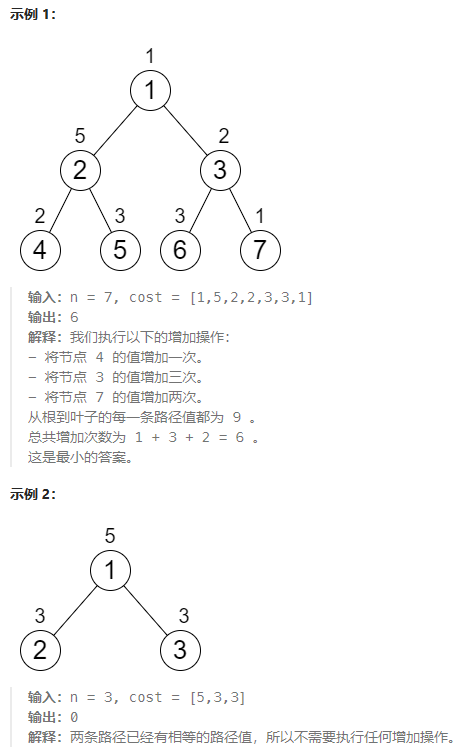
说明:
- 3 <= n <= 105
- n + 1 是 2 的幂
- cost.length == n
- 1 <= cost[i] <= 104
思路
操作首先要知道操作的最终状态:各路径相等。那么哪一个路径值可以使操作总数最小?既然明确不了哪一个路径又如何操作,又怎会知道最小?最开始以为可能是路径的中位数,但是我也没法证明。后来发现想复杂了,操作只能加不能减,那么问题就变成了将所有路径变成最大最少需要几次操作。
首先可以根据节点的父子关系将子路径值层层累加,那么最底下的叶子层就是各条路径的值。用最大路径值分别减去其它路径值得到相应的操作数,但这时操作数不是最小的。注意到,如果左右孩子所需操作均不为零,可以将较小孩子节点的操作数提到父节点上,并将操作数置零,而另一个孩子节点同时减去该操作数,这样就完成了一步最小化。依次向上计算,直到根节点,然后统计各节点操作数即可。
代码
/**
* @date 2024-02-28 8:52
*/
public class MinIncrements {
public int minIncrements(int n, int[] cost) {
for (int i = 1; i < cost.length; i++) {
if (i % 2 == 1) {
cost[i] += cost[(i - 1) / 2];
} else {
cost[i] += cost[(i - 2) / 2];
}
}
int max = 0;
double l = Math.floor(Math.log(Double.parseDouble(String.valueOf(n))) / Math.log(2.0));
for (int i = (int) Math.pow(2.0, l) - 1; i < cost.length; i++) {
if (cost[i] > max) {
max = cost[i];
}
}
for (int i = (int) Math.pow(2.0, l) - 1; i < cost.length; i++) {
cost[i] = max - cost[i];
}
for (int i = cost.length - 1; i > 2; i -= 2) {
if (cost[i] == 0 || cost[i - 1] == 0) {
cost[(i - 2) / 2] = 0;
continue;
}
if (cost[i] <= cost[i - 1]) {
cost[(i - 2) / 2] = cost[i];
cost[i - 1] = cost[i - 1] - cost[i];
cost[i] = 0;
} else if (cost[i] >= cost[i - 1]) {
cost[(i - 2) / 2] = cost[i - 1];
cost[i] = cost[i] - cost[i - 1];
cost[i - 1] = 0;
}
}
int res = 0;
for (int i = 1; i < cost.length; i++) {
res += cost[i];
}
return res;
}
public static void main(String[] args) {
MinIncrements main = new MinIncrements();
// int[] cost = new int[]{1, 5, 2, 2, 3, 3, 1};
int[] cost = new int[]{764, 1460, 2664, 764, 2725, 4556, 5305, 8829, 5064, 5929, 7660, 6321, 4830, 7055, 3761};
System.out.println(main.minIncrements(cost.length, cost));
}
}
性能

又是勉强过关。看看官网给的答案:
class Solution {
public int minIncrements(int n, int[] cost) {
int ans = 0;
for (int i = n - 2; i > 0; i -= 2) {
ans += Math.abs(cost[i] - cost[i + 1]);
// 叶节点 i 和 i+1 的双亲节点下标为 i/2(整数除法)
cost[i / 2] += Math.max(cost[i], cost[i + 1]);
}
return ans;
}
}称之为自底向上的贪心算法。所谓贪心算法,它在每一步都做出当时看起来最佳的选择,也就是说,它总是做出局部最优的选择。贪心算法并不保证得到最优解,但对很多问题确实可以求得最优解。