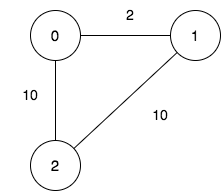
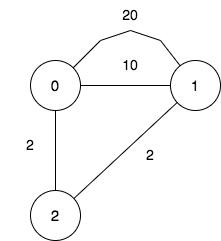
目标
给你一个大小为 3 * 3 ,下标从 0 开始的二维整数矩阵 grid ,分别表示每一个格子里石头的数目。网格图中总共恰好有 9 个石头,一个格子里可能会有 多个 石头。
每一次操作中,你可以将一个石头从它当前所在格子移动到一个至少有一条公共边的相邻格子。
请你返回每个格子恰好有一个石头的 最少移动次数 。
示例 1:
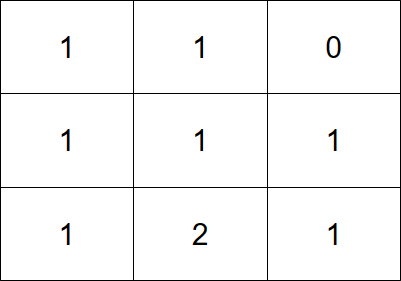
输入:grid = [[1,1,0],[1,1,1],[1,2,1]]
输出:3
解释:让每个格子都有一个石头的一个操作序列为:
1 - 将一个石头从格子 (2,1) 移动到 (2,2) 。
2 - 将一个石头从格子 (2,2) 移动到 (1,2) 。
3 - 将一个石头从格子 (1,2) 移动到 (0,2) 。
总共需要 3 次操作让每个格子都有一个石头。
让每个格子都有一个石头的最少操作次数为 3 。
示例 2:
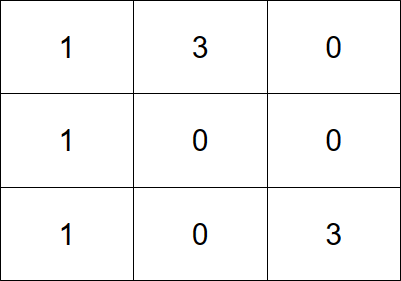
输入:grid = [[1,3,0],[1,0,0],[1,0,3]]
输出:4
解释:让每个格子都有一个石头的一个操作序列为:
1 - 将一个石头从格子 (0,1) 移动到 (0,2) 。
2 - 将一个石头从格子 (0,1) 移动到 (1,1) 。
3 - 将一个石头从格子 (2,2) 移动到 (1,2) 。
4 - 将一个石头从格子 (2,2) 移动到 (2,1) 。
总共需要 4 次操作让每个格子都有一个石头。
让每个格子都有一个石头的最少操作次数为 4 。
说明:
- grid.length == grid[i].length == 3
0 <= grid[i][j] <= 9- grid 中元素之和为 9 。
思路
有一个3 * 3 的二维矩阵,有9个石头散落在其中,每次可以将石头移到相邻的格子里,问每个格子一块石头最少需要移动几次。
有多余石头的格子到没有石头格子移动的次数为其曼哈顿距离,要想使移动次数最小,我们只需要从没有石头的格子向四个方向查找有多余石头的格子即可。
并非是沿四个方向搜索,而是BFS找最短路径。 遍历四个方向,那么只能沿着该方向查找,而BFS则是由内层向外层查找,体会二者的不同。但这题使用BFS也无法保证得到的是最小移动次数,考虑下面的情况:
从0开始取最近的并不能保证得到最优解,比如下面这种情况:
3,2,0 3,1,1 2,1,1 2,1,1 2,1,1 1,1,1
0,1,0 -> 0,1,0 -> 1,1,0 -> 1,1,1 -> 1,1,1 -> 1,1,1
0,3,0 0,3,0 0,3,0 0,2,0 1,1,0 1,1,1
1 1 2 1 4
左下角的应该从第一个元素取:
3,2,0 3,1,1 2,1,1 2,1,1 1,1,1 1,1,1
0,1,0 -> 0,1,0 -> 1,1,0 -> 1,1,1 -> 1,1,1 -> 1,1,1
0,3,0 0,3,0 0,3,0 0,2,0 1,2,0 1,1,1
1 1 2 2 1
尽管这题使用BFS求解不了,但还是有一些收获的。BFS很容易错写成每次从队列取一个元素,然后判断该元素是否满足条件,不满足就将其邻接节点加入队列。当需要进行层次计数的时候就不对了,应该在每次循环的第一步记录队列中元素个数 k,本次处理中就循环判断这k个元素,在循环过程中判断是否满足条件,不满足的将其邻接节点加入队列,因为我们已经在前面计数了,因此这些邻接节点将在下一次循环中处理。
如果取最近的多余石头这种贪心策略不行的话,那么问题就不在于最短路径了。而应从整体上考虑从哪里移动到哪里才是最优的,可以尝试记忆化搜索解空间。我们可以很容易枚举出哪些格子没有石头,哪些格子石头多于1个,只需枚举它们的组合并取其曼哈顿距离之和最小值即可。
这里的核心问题是如何遍历这两个列表的组合,我想到的方法就是使用回溯算法,每向下递归一层就标记为已访问,而返回时再取消其标记。并且如果不保存重复子问题的话,执行会超时。这里的重复子问题是两组数据未访问元素相同,而已访问数据的组合不同。例如: [a,b,c,d,e,f,g] [h,i,j,k,l,m,n] 前面两个元素组合 (a, h) (b, i) 与 (a, i) (b, h) 剩余的元素的组合情况完全相同。
最终使用状态压缩与回溯解出来了。如果不记录重复的子问题的话,dfs方法要调用3705927296次,而使用记忆化搜索只需调用12868次。
官网题解也是类似的思路,只不过遍历组合的方式不同,它是固定一个列表不变,另一个进行全排列。//todo 有空再研究一下官网题解吧
代码
/**
* @date 2024-07-20 15:55
*/
public class MinimumMoves2850 {
public int minimumMoves_v2(int[][] grid) {
List<int[]> zeros = new ArrayList<>();
List<int[]> more = new ArrayList<>();
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (grid[i][j] == 0) {
zeros.add(new int[]{i, j});
} else if (grid[i][j] > 1) {
for (int k = 0; k < grid[i][j] - 1; k++) {
more.add(new int[]{i, j});
}
}
}
}
int k = zeros.size();
int res = Integer.MAX_VALUE;
int[][] mem = new int[255][255];
for (int i = 0; i < k; i++) {
// 状态压缩
int zerosVisited = 0x000000ff;
zerosVisited ^= 1 << i;
int[] zero = zeros.get(i);
for (int j = 0; j < k; j++) {
int moreVisited = 0x000000ff;
moreVisited ^= 1 << j;
int[] m = more.get(j);
int distance = Math.abs(zero[0] - m[0]) + Math.abs(zero[1] - m[1]);
res = Math.min(res, distance + dfs_v2(zeros, more, zerosVisited, moreVisited, 1, mem));
}
}
return res;
}
public int dfs_v2(List<int[]> zeros, List<int[]> more, int zerosVisited, int moreVisited, int level, int[][] mem) {
if (level == zeros.size()) {
return 0;
}
int k = zeros.size();
int res = Integer.MAX_VALUE;
for (int i = 0; i < k; i++) {
if (((zerosVisited >> i) & 1) == 0) {
continue;
}
zerosVisited ^= 1 << i;
int[] zero = zeros.get(i);
for (int j = 0; j < k; j++) {
if (((moreVisited >> j) & 1) == 0) {
continue;
}
moreVisited ^= 1 << j;
int[] m = more.get(j);
int distance = Math.abs(zero[0] - m[0]) + Math.abs(zero[1] - m[1]);
if (mem[zerosVisited][moreVisited] == 0) {
// 重复的子问题是两边剩余的元素均相同
mem[zerosVisited][moreVisited] = dfs_v2(zeros, more, zerosVisited, moreVisited, level + 1, mem);
}
res = Math.min(res, distance + mem[zerosVisited][moreVisited]);
// 回溯
moreVisited ^= 1 << j;
}
zerosVisited ^= 1 << i;
}
return res;
}
}
性能