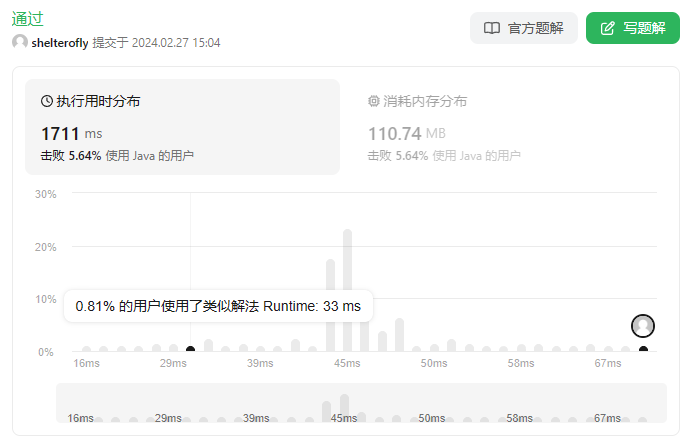
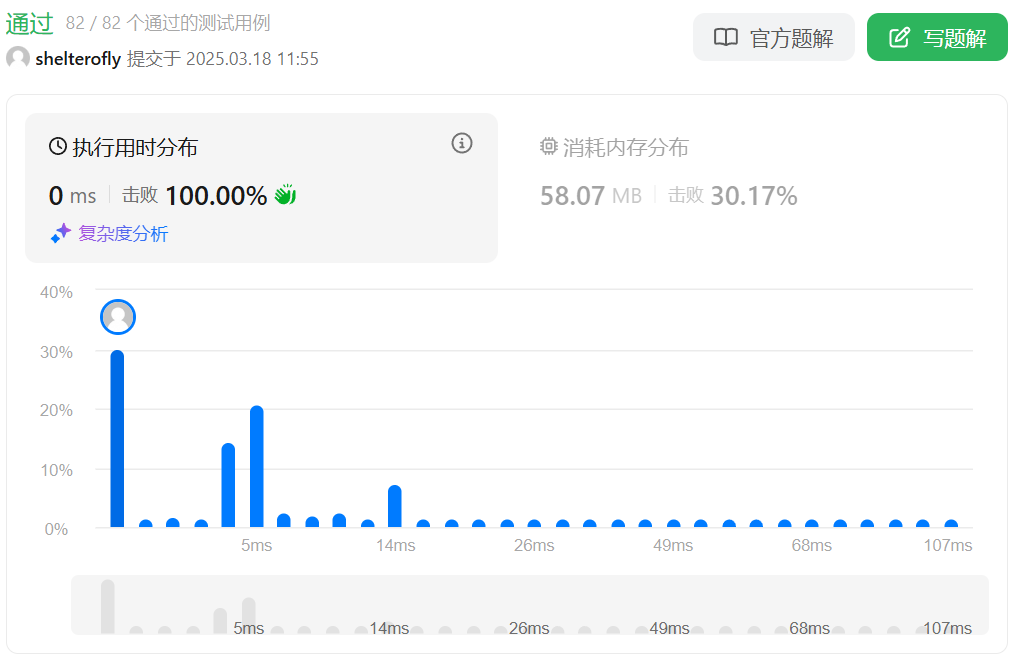
目标
给你一棵 n 个节点的无向树,节点编号为 1 到 n 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示节点 ui 和 vi 在树中有一条边。
请你返回树中的 合法路径数目 。
如果在节点 a 到节点 b 之间 恰好有一个 节点的编号是质数,那么我们称路径 (a, b) 是 合法的 。
注意:
- 路径 (a, b) 指的是一条从节点 a 开始到节点 b 结束的一个节点序列,序列中的节点 互不相同 ,且相邻节点之间在树上有一条边。
- 路径 (a, b) 和路径 (b, a) 视为 同一条 路径,且只计入答案 一次 。
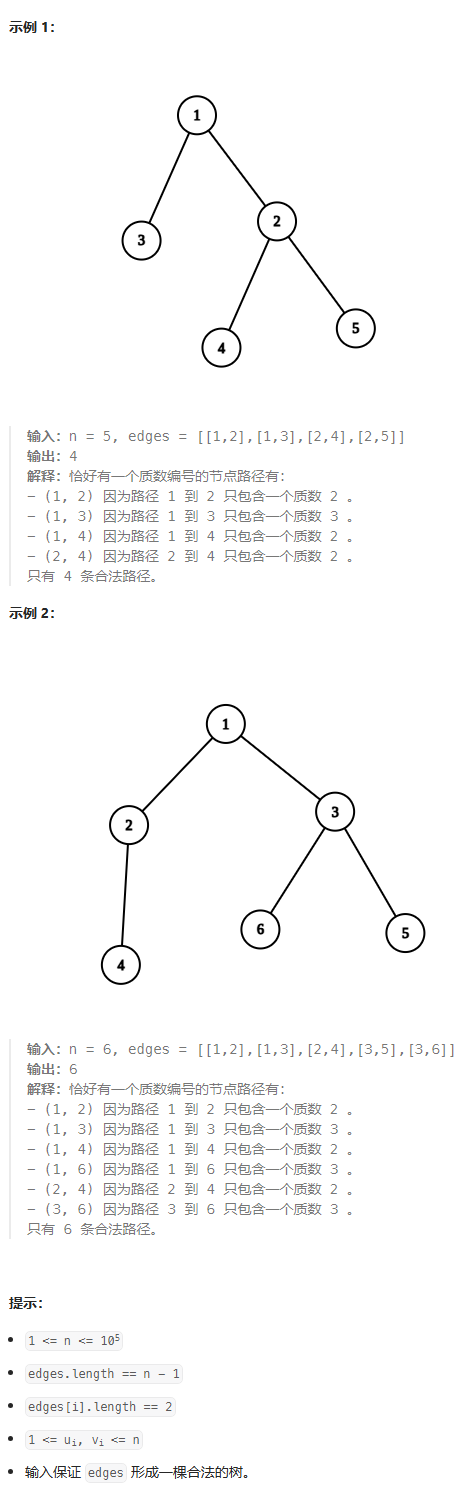
思路
质数是指在大于1的自然数(非负整数)中,除了1和它本身以外不再有其他因数的自然数。
现在有一颗 n 个节点的无向树,要求任意两个连通节点间恰好有一个质数节点的路径数。树是一种无环连通图,问题可以转化为从树中选取两个节点,节点之间的路径只经过一个质数节点。由于没有环,所以两点之间的路径是唯一的。
- 两个都是质数节点要排除掉。
- 以质数节点为中心,与它邻接的非质数节点符合条件。即以质数节点为中心加上与之相连的非质数节点任取两个均可。我们可以称直接与质数节点相连的非质数节点为直接节点。
- 直接节点连通的非质数节点也可能满足条件,需要要减去直接节点向外连通的路径,即直接节点加上其向外连通的节点之间任取两个的路径数。
按照上面的思路,先要找到所有的质数节点,涉及到质数判断。同时保存与之直接相连的非质数节点。然后保存非质数节点的边,使用Map保存,边的两个端点都保存进去,方便后续向外查找连通的节点。
得到满足条件的节点总数,根据排列组合公式C(n,2) = n!/(2!(n-2)!) = (n-1)n/2 求得路径总数D。
将外围节点k向外连通节点总数记为Ik,无效路径数为(Ik-1)Ik/2。
最终的结果就是D - Σ(Ik-1)Ik/2
代码
/**
* @date 2024-02-27 0:22
*/
public class CountPaths {
public Map<Integer, Set<Integer>> primeEdges = new HashMap<>();
public Map<Integer, Set<Integer>> notPrimeEdges = new HashMap<>();
public Map<Integer, Integer> indirectNodesNumMap = new HashMap<>();
Set<Integer> counter = new HashSet<>();
public long countPaths(int n, int[][] edges) {
for (int i = 0; i < n - 1; i++) {
int[] edge = edges[i];
boolean i0 = isPrimeNumber(edge[0]);
boolean i1 = isPrimeNumber(edge[1]);
if (i0 && !i1) {
primeEdges.computeIfAbsent(edge[0], k -> new HashSet<>());
primeEdges.get(edge[0]).add(edge[1]);
} else if (!i0 && i1) {
primeEdges.computeIfAbsent(edge[1], k -> new HashSet<>());
primeEdges.get(edge[1]).add(edge[0]);
} else if(!i0){
notPrimeEdges.computeIfAbsent(edge[0], k -> new HashSet<>());
notPrimeEdges.computeIfAbsent(edge[1], k -> new HashSet<>());
notPrimeEdges.get(edge[0]).add(edge[1]);
notPrimeEdges.get(edge[1]).add(edge[0]);
}
}
long res = 0;
for (Integer primeNode : primeEdges.keySet()) {
Set<Integer> nonPrimeNodesOfPrimeEdge = primeEdges.get(primeNode);
counter.clear();
int total = 0;
for (int nonPrimeNode : nonPrimeNodesOfPrimeEdge) {
counter.add(nonPrimeNode);
if (indirectNodesNumMap.get(nonPrimeNode) == null) {
indirectNodesNumMap.put(nonPrimeNode, 1);
countEdges(nonPrimeNode, nonPrimeNode);
}
total += indirectNodesNumMap.get(nonPrimeNode);
}
total = total + 1;
res += total * (total - 1L) / 2L;
for (int nonPrimeNode : nonPrimeNodesOfPrimeEdge) {
int indirectNodesNum = indirectNodesNumMap.get(nonPrimeNode);
res -= indirectNodesNum * (indirectNodesNum - 1L) / 2L;
}
}
return res;
}
public Set<Integer> countEdges(int key, int nonPrimeNode) {
if (notPrimeEdges.get(nonPrimeNode) != null) {
for (Integer node : notPrimeEdges.get(nonPrimeNode)) {
if (!counter.contains(node)) {
indirectNodesNumMap.put(key, indirectNodesNumMap.get(key) + 1);
counter.add(node);
countEdges(key, node);
}
}
}
return counter;
}
public boolean isPrimeNumber(int num) {
if (num == 1) {
return false;
}
if (num == 2) {
return true;
}
if (num % 2 == 0) {
return false;
}
for (int i = 3; i * i <= num; i+=2) {
if (num % i == 0) {
return false;
}
}
return true;
}
public static void main(String[] args) {
// int[][] edges = new int[][]{new int[]{1, 2}, new int[]{1, 3}, new int[]{2, 4}, new int[]{2, 5}};
int[][] edges = new int[][]{new int[]{1, 2}, new int[]{4, 1}, new int[]{3, 4}};
CountPaths main = new CountPaths();
// System.out.println(main.countPaths(5, edges));
System.out.println(main.countPaths(4, edges));
}
}
性能
勉强通过。有时间再回来看看题解吧。