目标
给你一个有 n 个节点的 有向带权 图,节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示,其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。
请你实现一个 Graph 类:
- Graph(int n, int[][] edges) 初始化图有 n 个节点,并输入初始边。
- addEdge(int[] edge) 向边集中添加一条边,其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。
- int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径 最小 代价。如果路径不存在,返回 -1 。一条路径的代价是路径中所有边代价之和。
示例 1:
输入:
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
输出:
[null, 6, -1, null, 6]
解释:
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示:3 -> 0 -> 1 -> 2 ,总代价为 3 + 2 + 1 = 6 。
g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。
g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边,得到第二幅图。
g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ,总代价为 2 + 4 = 6 。说明:
- 1 <= n <= 100
- 0 <= edges.length <= n * (n - 1)
- edges[i].length == edge.length == 3
- 0 <= fromi, toi, from, to, node1, node2 <= n - 1
- 1 <= edgeCosti, edgeCost <= 10^6
- 图中任何时候都不会有重边和自环。
- 调用 addEdge 至多 100 次。
- 调用 shortestPath 至多 100 次。
思路
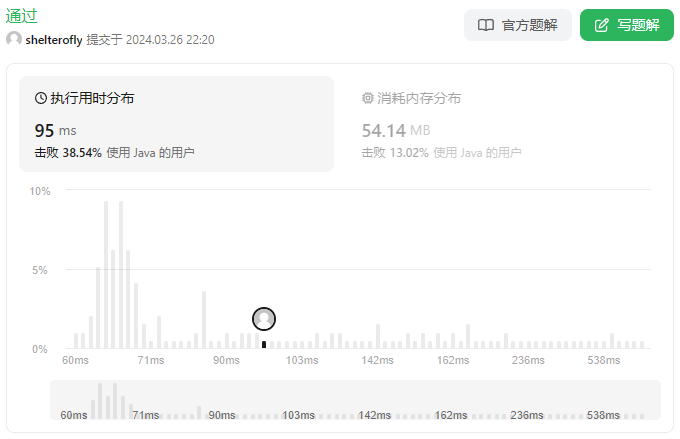
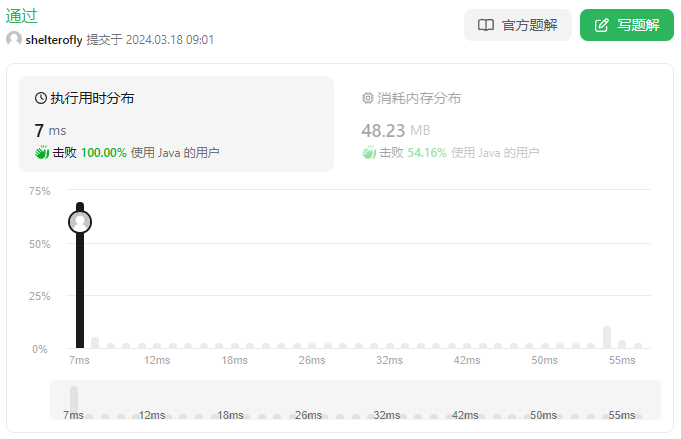
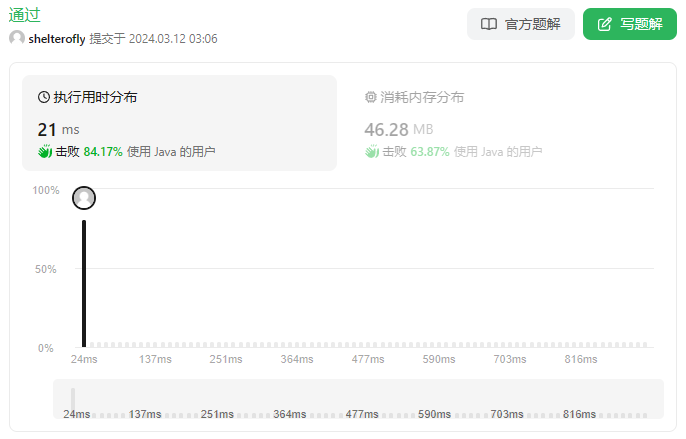
今天又手写了一遍Dijkstra算法,虽然通过了,但是性能差好多。对照着官网题解研究了一会,我也想把一些优化的点表达出来,但还是感觉没有理解透彻。又看了耗时最少的题解一脸懵,也看到了网友讲解的朴素 Dijkstra算法,有机会再研究补上吧。
代码
/**
* @date 2024-03-26 8:35
*/
public class Graph {
private final ArrayList<int[]>[] g;
private PriorityQueue<int[]> q;
private int[] dp;
private int n;
public Graph(int n, int[][] edges) {
g = new ArrayList[n];
for (int i = 0; i < g.length; i++) {
g[i] = new ArrayList<>();
}
for (int i = 0; i < edges.length; i++) {
g[edges[i][0]].add(new int[]{edges[i][1], edges[i][2]});
}
this.n = n;
}
public void addEdge(int[] edge) {
g[edge[0]].add(new int[]{edge[1], edge[2]});
}
public int shortestPath(int node1, int node2) {
q = new PriorityQueue<int[]>((a, b) -> a[1] - b[1]);
dp = new int[n];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[node1] = 0;
q.offer(new int[]{node1, 0});
while (!q.isEmpty()) {
int[] e = q.poll();
if (e[0] == node2) {
return dp[node2];
}
for (int[] edge : g[e[0]]) {
if (dp[e[0]] + edge[1] < dp[edge[0]]) {
dp[edge[0]] = dp[e[0]] + edge[1];
q.offer(new int[]{edge[0], dp[edge[0]]});
}
}
}
return dp[node2] == Integer.MAX_VALUE ? -1 : dp[node2];
}
}
性能