标签： 数学

目标

银行内部的防盗安全装置已经激活。给你一个下标从 0 开始的二进制字符串数组 bank ，表示银行的平面图，这是一个大小为 m x n 的二维矩阵。 bank[i] 表示第 i 行的设备分布，由若干 '0' 和若干 '1' 组成。'0' 表示单元格是空的，而 '1' 表示单元格有一个安全设备。

对任意两个安全设备而言，如果同时 满足下面两个条件，则二者之间存在 一个 激光束：

• 两个设备位于两个 不同行 ：r1 和 r2 ，其中 r1 < r2 。
• 满足 r1 < i < r2 的 所有 行 i ，都 没有安全设备 。

激光束是独立的，也就是说，一个激光束既不会干扰另一个激光束，也不会与另一个激光束合并成一束。

返回银行中激光束的总数量。

示例 1：

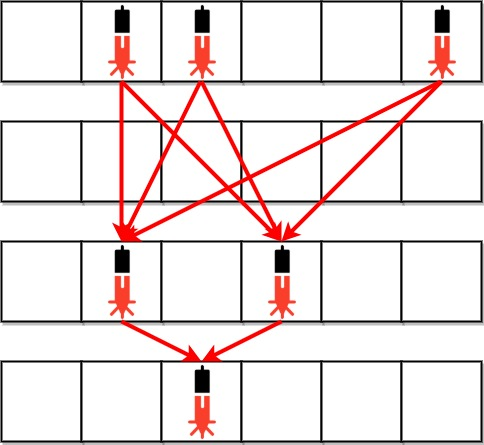
输入：bank = ["011001","000000","010100","001000"]
输出：8
解释：在下面每组设备对之间，存在一条激光束。总共是 8 条激光束：
 * bank[0][1] -- bank[2][1]
 * bank[0][1] -- bank[2][3]
 * bank[0][2] -- bank[2][1]
 * bank[0][2] -- bank[2][3]
 * bank[0][5] -- bank[2][1]
 * bank[0][5] -- bank[2][3]
 * bank[2][1] -- bank[3][2]
 * bank[2][3] -- bank[3][2]
注意，第 0 行和第 3 行上的设备之间不存在激光束。
这是因为第 2 行存在安全设备，这不满足第 2 个条件。

示例 2：

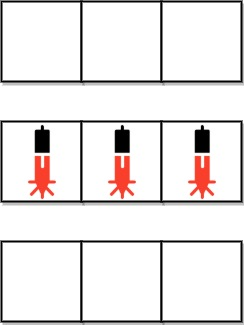
输入：bank = ["000","111","000"]
输出：0
解释：不存在两个位于不同行的设备

提示：

• m == bank.length
• n == bank[i].length
• 1 <= m, n <= 500
• bank[i][j] 为 '0' 或 '1'

思路

跳过中间的空行，将相邻的非空行上的装置数量相乘。

代码

/**
 * @date 2025-10-27 10:34
 */
public class NumberOfBeams2125 {

    public int numberOfBeams(String[] bank) {
        int prev = 0, cur = 0;
        int res = 0;
        for (String b : bank) {
            for (char c : b.toCharArray()) {
                if (c == '1') {
                    cur++;
                }
            }
            if (cur == 0) {
                continue;
            }
            res += cur * prev;
            prev = cur;
            cur = 0;
        }
        return res;
    }

}

性能

目标

给你一个下标从 0 开始的整数数组 nums 和一个整数 value 。

在一步操作中，你可以对 nums 中的任一元素加上或减去 value 。

• 例如，如果 nums = [1,2,3] 且 value = 2 ，你可以选择 nums[0] 减去 value ，得到 nums = [-1,2,3] 。

数组的 MEX (minimum excluded) 是指其中数组中缺失的最小非负整数。

• 例如，[-1,2,3] 的 MEX 是 0 ，而 [1,0,3] 的 MEX 是 2 。

返回在执行上述操作 任意次 后，nums 的最大 MEX 。

示例 1：

输入：nums = [1,-10,7,13,6,8], value = 5
输出：4
解释：执行下述操作可以得到这一结果：
- nums[1] 加上 value 两次，nums = [1,0,7,13,6,8]
- nums[2] 减去 value 一次，nums = [1,0,2,13,6,8]
- nums[3] 减去 value 两次，nums = [1,0,2,3,6,8]
nums 的 MEX 是 4 。可以证明 4 是可以取到的最大 MEX 。

示例 2：

输入：nums = [1,-10,7,13,6,8], value = 7
输出：2
解释：执行下述操作可以得到这一结果：
- nums[2] 减去 value 一次，nums = [1,-10,0,13,6,8]
nums 的 MEX 是 2 。可以证明 2 是可以取到的最大 MEX 。

说明：

• 1 <= nums.length, value <= 10^5
• -10^9 <= nums[i] <= 10^9

思路

有一个数组，可以执行 任意 次操作，每次操作可以将任意元素加上或者减去 value，求数组中缺失的最小非负整数的最大值。

题目要求返回缺失的最小非负整数，可以从 0 开始枚举每一个整数 target，问题是如何判断数组中是否存在元素 nums[i] + k * value == target。两边同时对 value 取余可得 nums[i] ≡ target (mod value)。

可以对 nums[i] % value 计数，枚举 target 判断是否还剩有同余元素即可。

代码

/**
 * @date 2025-10-16 8:46
 */
public class FindSmallestInteger2598 {

    public int findSmallestInteger(int[] nums, int value) {
        int[] cnt = new int[value];
        for (int num : nums) {
            int rem = num % value;
            rem = rem >= 0 ? rem : rem + value;
            cnt[rem]++;
        }
        int res = 0;
        while (true) {
            int rem = res % value;
            if (cnt[rem] > 0) {
                cnt[rem]--;
            } else {
                return res;
            }
            res++;
        }
    }

}

性能

目标

给定两个整数，分别表示分数的分子 numerator 和分母 denominator，以 字符串形式返回小数 。

如果小数部分为循环小数，则将循环的部分括在括号内。

如果存在多个答案，只需返回 任意一个 。

对于所有给定的输入，保证 答案字符串的长度小于 10^4 。

示例 1：

输入：numerator = 1, denominator = 2
输出："0.5"

示例 2：

输入：numerator = 2, denominator = 1
输出："2"

示例 3：

输入：numerator = 4, denominator = 333
输出："0.(012)"

说明：

• -2^31 <= numerator, denominator <= 2^31 - 1
• denominator != 0

思路

有一个分数，分子分母均为整数，以字符串的形式返回小数，如果是循环小数，将循环部分括在括号内。

关键是如何确定从哪里开始循环？记录余数对应的商的下标，如果余数重复出现说明进入了循环节，根据下标来找出循环节。

代码

/**
 * @date 2025-09-24 9:13
 */
public class FractionToDecimal166 {

    public String fractionToDecimal_v1(int numerator, int denominator) {
        long a = numerator;
        long b = denominator;
        if (a % b == 0) {
            return String.valueOf(a / b);
        }
        StringBuilder sb = new StringBuilder();
        if (a * b < 0) {
            sb.append("-");
        }
        a = Math.abs(a);
        b = Math.abs(b);
        long d = a / b;
        sb.append(d);
        long rem = a % b;
        sb.append(".");
        StringBuilder fraction = new StringBuilder();
        Map<Long, Integer> map = new HashMap<>();
        int i = 0;
        while (rem != 0) {
            if (map.get(rem) != null) {
                return sb.append(fraction.substring(0, map.get(rem)))
                        .append("(")
                        .append(fraction.substring(map.get(rem)))
                        .append(")").toString();
            }
            map.put(rem, i);
            rem *= 10;
            if (rem < b) {
                fraction.append(0);
            } else {
                d = rem / b;
                fraction.append(d);
                rem = rem % b;
            }
            i++;
        }
        return sb.append(fraction).toString();
    }

}

性能

目标

给你一个整数数组 nums ，返回全部为 0 的 子数组 数目。

子数组 是一个数组中一段连续非空元素组成的序列。

示例 1：

输入：nums = [1,3,0,0,2,0,0,4]
输出：6
解释：
子数组 [0] 出现了 4 次。
子数组 [0,0] 出现了 2 次。
不存在长度大于 2 的全 0 子数组，所以我们返回 6 。

示例 2：

输入：nums = [0,0,0,2,0,0]
输出：9
解释：
子数组 [0] 出现了 5 次。
子数组 [0,0] 出现了 3 次。
子数组 [0,0,0] 出现了 1 次。
不存在长度大于 3 的全 0 子数组，所以我们返回 9 。

示例 3：

输入：nums = [2,10,2019]
输出：0
解释：没有全 0 子数组，所以我们返回 0 。

说明：

• 1 <= nums.length <= 10^5
• -10^9 <= nums[i] <= 10^9

思路

返回数组的全 0 子数组个数。

长度为 k 的子数组个数为 (1 + k) * k / 2。可以使用贪心策略，如果当前元素是 0 找到以它为起点的最长连续 0 数组，计算子数组个数。

代码

/**
 * @date 2025-08-19 8:54
 */
public class ZeroFilledSubarray2348 {

    public long zeroFilledSubarray(int[] nums) {
        long res = 0L;
        int n = nums.length;
        int i = 0;
        while (i < n){
            if (nums[i] != 0){
                i++;
                continue;
            }
            int start = i;
            while (i < n && nums[i] == 0){
                i++;
            }
            int cnt = i - start;
            res += (1L + cnt) * cnt / 2;
        }

        return res;
    }
}

性能