标签： 数学

目标

给你一个二维整数数组 points，其中 points[i] = [xi, yi] 表示第 i 个点在笛卡尔平面上的坐标。

水平梯形 是一种凸四边形，具有 至少一对 水平边（即平行于 x 轴的边）。两条直线平行当且仅当它们的斜率相同。

返回可以从 points 中任意选择四个不同点组成的 水平梯形 数量。

由于答案可能非常大，请返回结果对 10^9 + 7 取余数后的值。

示例 1：

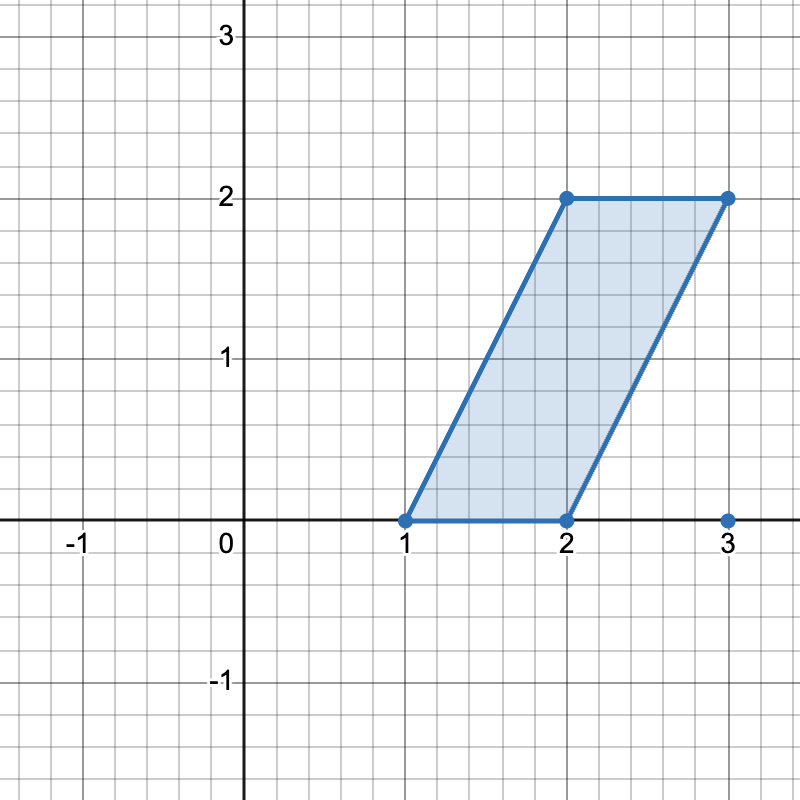
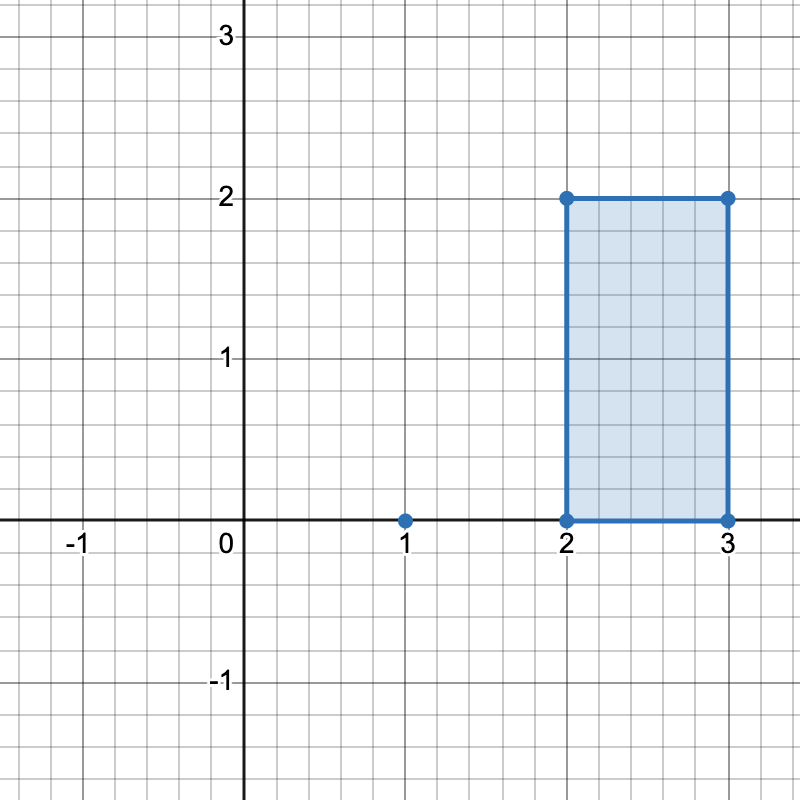
输入： points = [[1,0],[2,0],[3,0],[2,2],[3,2]]
输出： 3
解释：
有三种不同方式选择四个点组成一个水平梯形：
使用点 [1,0]、[2,0]、[3,2] 和 [2,2]。
使用点 [2,0]、[3,0]、[3,2] 和 [2,2]。
使用点 [1,0]、[3,0]、[3,2] 和 [2,2]。

示例 2：

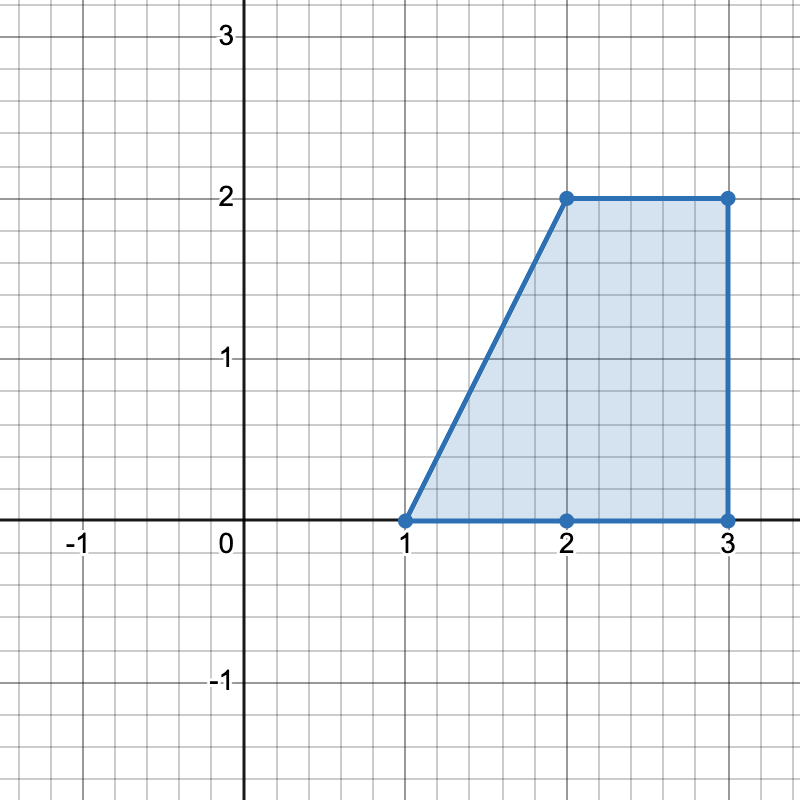
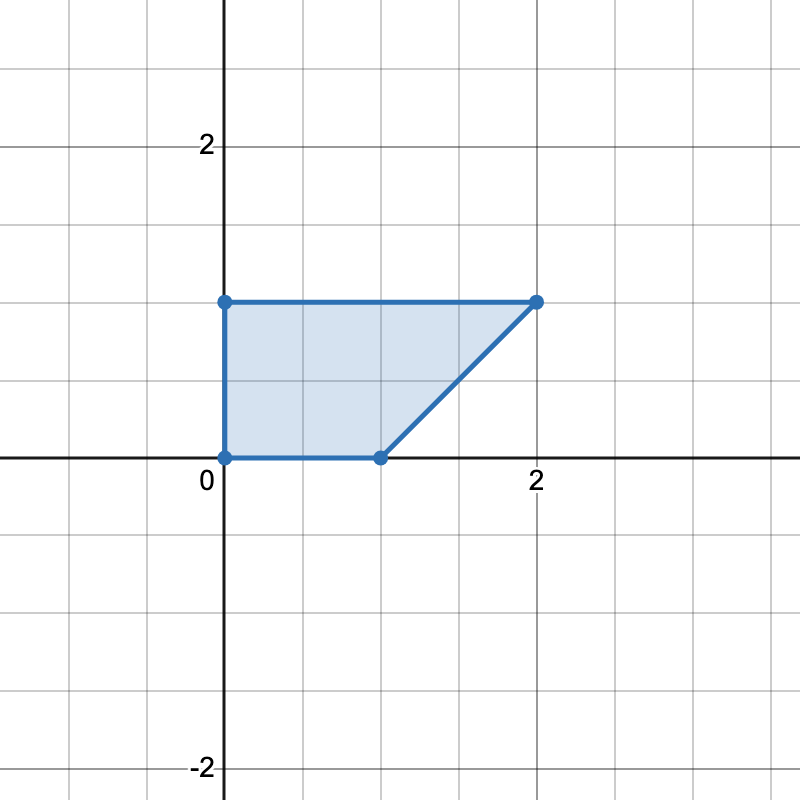
输入： points = [[0,0],[1,0],[0,1],[2,1]]
输出： 1
解释：
只有一种方式可以组成一个水平梯形。

说明：

• 4 <= points.length <= 10^5
• –10^8 <= xi, yi <= 10^8
• 所有点两两不同。

思路

有一些二维平面中的点 points，从中选取四个点组成水平梯形，返回水平梯形的数目。

水平梯形是有一对边平行于 x 轴的梯形。直接的想法是根据纵坐标分组，选两组，每组中选两个点。

可以直接计算每组的组合数 C(n, 2) = n * (n - 1) / 2，计算分组组合数的后缀和，根据乘法原理计算即可。

代码

/**
 * @date 2025-12-02 0:14
 */
public class CountTrapezoids2623 {

    /**
     * 执行通过
     */
    public int countTrapezoids(int[][] points) {
        Map<Integer, Integer> cnt = new HashMap<>();
        for (int[] point : points) {
            cnt.merge(point[1], 1, Integer::sum);
        }
        int mod = 1000000007;
        for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
            Integer c = entry.getValue();
            cnt.put(entry.getKey(), (int) ((c * (c - 1L) / 2) % mod));
        }
        int[] comb = cnt.values().stream().mapToInt(x -> x).toArray();
        int n = comb.length;
        int[] suffix = new int[n + 1];
        for (int i = n - 1; i >= 0; i--) {
            suffix[i] = (suffix[i + 1] + comb[i]) % mod;
        }
        long res = 0L;
        for (int i = 0; i < n; i++) {
            res = (res + ((long) comb[i] * suffix[i + 1])) % mod;
        }
        return (int) res;
    }
}

性能

目标

给定正整数 k ，你需要找出可以被 k 整除的、仅包含数字 1 的最 小 正整数 n 的长度。

返回 n 的长度。如果不存在这样的 n ，就返回-1。

注意： n 可能不符合 64 位带符号整数。

示例 1：

输入：k = 1
输出：1
解释：最小的答案是 n = 1，其长度为 1。

示例 2：

输入：k = 2
输出：-1
解释：不存在可被 2 整除的正整数 n 。

示例 3：

输入：k = 3
输出：3
解释：最小的答案是 n = 111，其长度为 3。

说明：

• 1 <= k <= 10^5

思路

求仅包含数字 1 且能够整除正整数 k 的数字的最小长度，如不存在返回 -1。

通俗讲就是多长的 11111…… 能够整除 k。为了防止溢出可以只考虑余数，关键是停止条件是什么？如何确定是否存在？

如果余数出现重复，由于计算的式子不变，后续会陷入循环。可以使用哈希表记录出现过的余数。或者循环 k 次，由于余数的范围只可能是 0 ~ k - 1 共 k 个，如果循环 k 次还没有使余数为 0，那么根据鸽巢原理一定存在重复的余数。

代码

/**
 * @date 2025-11-25 9:26
 */
public class SmallestRepunitDivByK1015 {

    public int smallestRepunitDivByK(int k) {
        if (k == 1) {
            return 1;
        }
        int res = 1;
        int num = 1;
        while (res < k) {
            num = (num * 10 + 1) % k;
            res++;
            if (num == 0) {
                return res;
            }
        }
        return -1;
    }
}

性能

目标

给你一个二进制字符串 s（仅由 '0' 和 '1' 组成的字符串）。

返回所有字符都为 1 的子字符串的数目。

由于答案可能很大，请你将它对 10^9 + 7 取模后返回。

示例 1：

输入：s = "0110111"
输出：9
解释：共有 9 个子字符串仅由 '1' 组成
"1" -> 5 次
"11" -> 3 次
"111" -> 1 次

示例 2：

输入：s = "101"
输出：2
解释：子字符串 "1" 在 s 中共出现 2 次

示例 3：

输入：s = "111111"
输出：21
解释：每个子字符串都仅由 '1' 组成

示例 4：

输入：s = "000"
输出：0

说明：

• s[i] == '0' 或 s[i] == '1'
• 1 <= s.length <= 10^5

思路

统计全一子串的个数。

根据等差数列求和公式计算即可。

代码

/**
 * @date 2025-11-16 22:17
 */
public class NumSub1513 {

    public int numSub(String s) {
        int mod = 1000000007;
        int n = s.length();
        int res = 0;
        for (int i = 0; i < n; i++) {
            if (s.charAt(i) == '0') {
                continue;
            }
            int start = i;
            while (i < n && s.charAt(i) == '1'){
                i++;
            }
            int cnt = i - start;
            res += ((cnt + 1L) * cnt / 2) % mod;

        }
        return res;
    }

}

性能

目标

给你一个下标从 0 开始的 正 整数数组 nums 。你可以对数组执行以下操作 任意 次：

• 选择一个满足 0 <= i < n - 1 的下标 i ，将 nums[i] 或者 nums[i+1] 两者之一替换成它们的最大公约数。

请你返回使数组 nums 中所有元素都等于 1 的 最少 操作次数。如果无法让数组全部变成 1 ，请你返回 -1 。

两个正整数的最大公约数指的是能整除这两个数的最大正整数。

示例 1：

输入：nums = [2,6,3,4]
输出：4
解释：我们可以执行以下操作：
- 选择下标 i = 2 ，将 nums[2] 替换为 gcd(3,4) = 1 ，得到 nums = [2,6,1,4] 。
- 选择下标 i = 1 ，将 nums[1] 替换为 gcd(6,1) = 1 ，得到 nums = [2,1,1,4] 。
- 选择下标 i = 0 ，将 nums[0] 替换为 gcd(2,1) = 1 ，得到 nums = [1,1,1,4] 。
- 选择下标 i = 2 ，将 nums[3] 替换为 gcd(1,4) = 1 ，得到 nums = [1,1,1,1] 。

示例 2：

输入：nums = [2,10,6,14]
输出：-1
解释：无法将所有元素都变成 1 。

说明：

• 2 <= nums.length <= 50
• 1 <= nums[i] <= 10^6

思路

有一个正整数数组 nums，每次操作可以将 nums[i] 或者 nums[i + 1] 替换成它们的最大公约数。求将 nums 所有元素变为 1 的最小操作次数，如果无法完成，返回 -1。

显然只要存在相邻的互质元素，就可以将其中的一个设置为 1，然后就可以将左右的元素按顺序替换为 1，总共需要操作 n 次。目标是如何用最小的操作次数使得存在一对相邻元素互质。暴力枚举 子数组 的起点与终点，计算所有元素的最大公约数，记录最小的子数组长度。

代码

/**
 * @date 2025-11-12 9:07
 */
public class MinOperations2654 {

    public int minOperations(int[] nums) {
        int n = nums.length;
        int res = Integer.MAX_VALUE;
        int oneCnt = 0;
        int gcdAll = nums[0];
        for (int num : nums) {
            if (num == 1) {
                oneCnt++;
            }
            gcdAll = gcd(gcdAll, num);
        }
        if (gcdAll > 1) {
            return -1;
        }
        if (oneCnt > 0) {
            return n - oneCnt;
        }
        for (int i = 0; i < n; i++) {
            int g = nums[i];
            for (int j = i; j < n; j++) {
                g = gcd(g, nums[j]);
                if (g == 1) {
                    res = Math.min(res, j - i + 1);
                    break;
                }
            }
        }
        return res - 2 + n;
    }

    public int gcd(int a, int b) {
        if (b == 0) {
            return a;
        }
        return gcd(b, a % b);
    }

}

性能