目标
在二维平面上存在 n 个矩形。给你两个下标从 0 开始的二维整数数组 bottomLeft 和 topRight,两个数组的大小都是 n x 2 ,其中 bottomLeft[i] 和 topRight[i] 分别代表第 i 个矩形的 左下角 和 右上角 坐标。
我们定义 向右 的方向为 x 轴正半轴(x 坐标增加),向左 的方向为 x 轴负半轴(x 坐标减少)。同样地,定义 向上 的方向为 y 轴正半轴(y 坐标增加),向下 的方向为 y 轴负半轴(y 坐标减少)。
你可以选择一个区域,该区域由两个矩形的 交集 形成。你需要找出能够放入该区域 内 的 最大 正方形面积,并选择最优解。
返回能够放入交集区域的正方形的 最大 可能面积,如果矩形之间不存在任何交集区域,则返回 0。
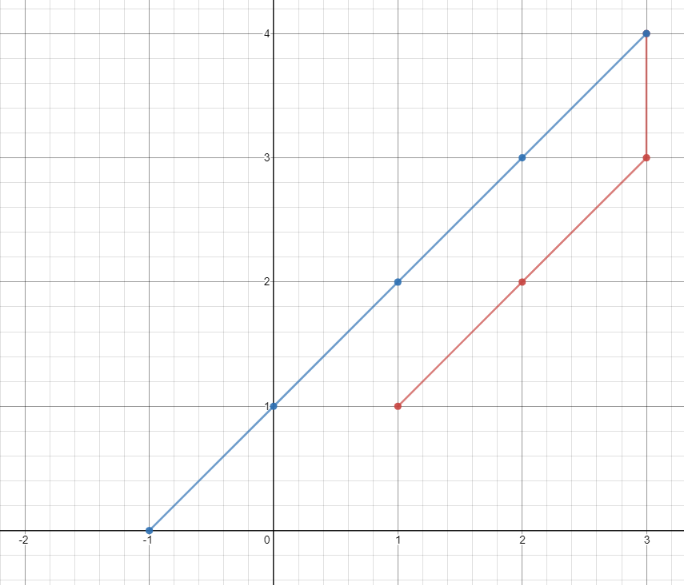
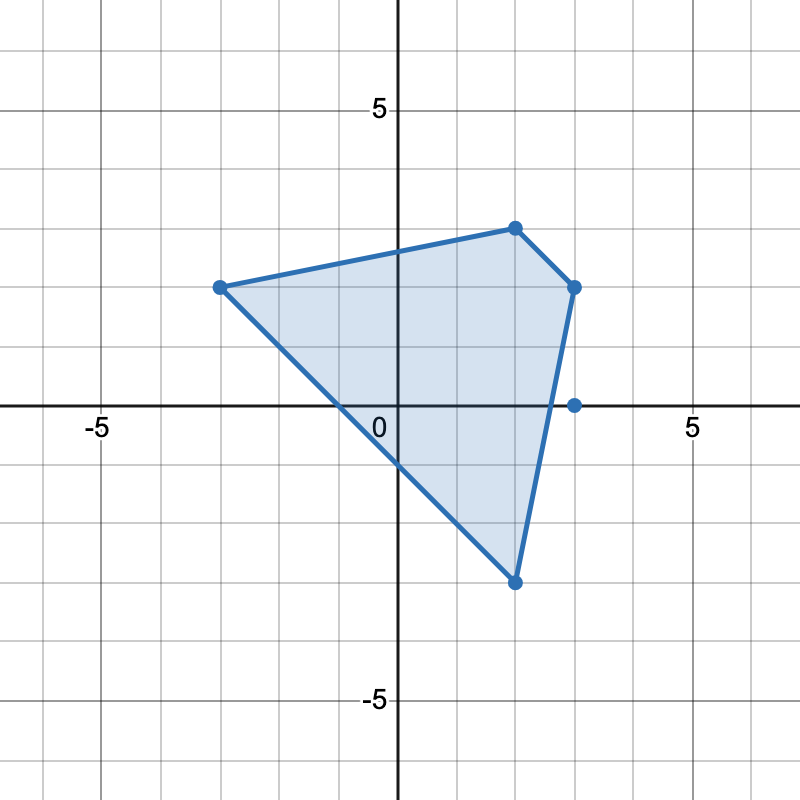
示例 1:

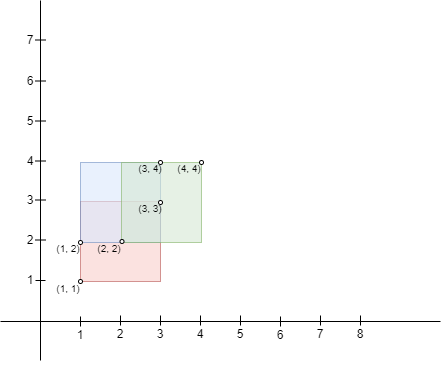
输入:bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
输出:1
解释:边长为 1 的正方形可以放入矩形 0 和矩形 1 的交集区域,或矩形 1 和矩形 2 的交集区域。因此最大面积是边长 * 边长,即 1 * 1 = 1。
可以证明,边长更大的正方形无法放入任何交集区域。示例 2:
输入:bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
输出:1
解释:边长为 1 的正方形可以放入矩形 0 和矩形 1,矩形 1 和矩形 2,或所有三个矩形的交集区域。因此最大面积是边长 * 边长,即 1 * 1 = 1。
可以证明,边长更大的正方形无法放入任何交集区域。
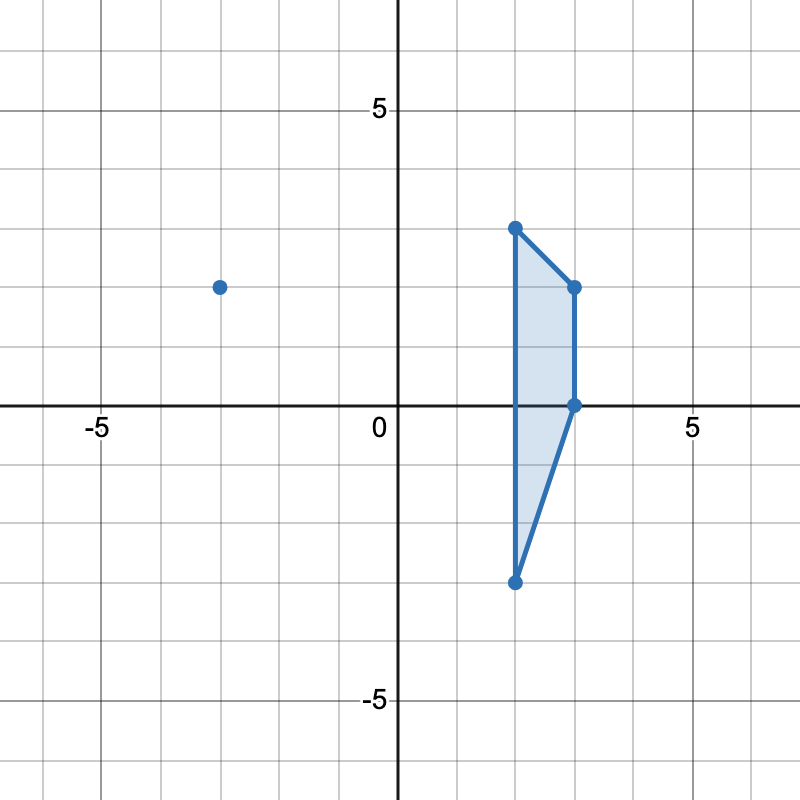
请注意,区域可以由多于两个矩形的交集构成。示例 3:
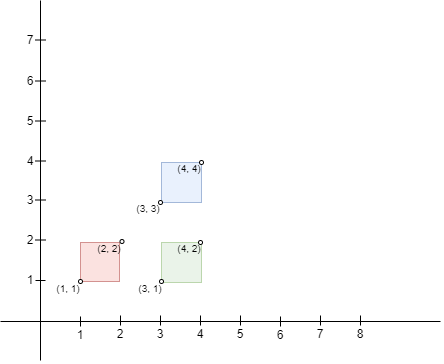
输入:bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
输出:0
解释:不存在相交的矩形,因此,返回 0 。说明:
- n == bottomLeft.length == topRight.length
- 2 <= n <= 10^3
- bottomLeft[i].length == topRight[i].length == 2
- 1 <= bottomLeft[i][0], bottomLeft[i][1] <= 10^7
- 1 <= topRight[i][0], topRight[i][1] <= 10^7
- bottomLeft[i][0] < topRight[i][0]
- bottomLeft[i][1] < topRight[i][1]
思路
二维平面上有一些矩形,第 i 个矩形的左下坐标为 bottomLeft[i],右上坐标为 topRight[i],求其中任意两个矩形交集区域的最大正方形面积。
针对每一个矩形,枚举其它矩形,计算交集区域最大的正方形边长。
令 bl1 表示矩形 1 的左下坐标,tr1 表示矩形 1 的右上坐标,bl2、tr2 同理。
- 相交区域的垂直边长为 Math.min(tr1[1], tr2[1]) - Math.max(bl1[1], bl2[1])
- 相交区域的水平边长为 Math.min(tr1[0], tr2[0]) - Math.max(bl1[0], bl2[0])
代码
/**
* @date 2026-01-21 9:08
*/
public class LargestSquareArea3047 {
public long largestSquareArea_v1(int[][] bottomLeft, int[][] topRight) {
long res = 0L;
int n = bottomLeft.length;
for (int i = 0; i < n; i++) {
int[] bl1 = bottomLeft[i], tr1 = topRight[i];
for (int j = i + 1; j < n; j++) {
int[] bl2 = bottomLeft[j], tr2 = topRight[j];
res = Math.max(res, Math.min(Math.min(tr1[1], tr2[1]) - Math.max(bl1[1], bl2[1]), Math.min(tr1[0], tr2[0]) - Math.max(bl1[0], bl2[0])));
}
}
return res * res;
}
}
性能