标签： 拓扑排序

目标

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。

给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。

请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。

如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。

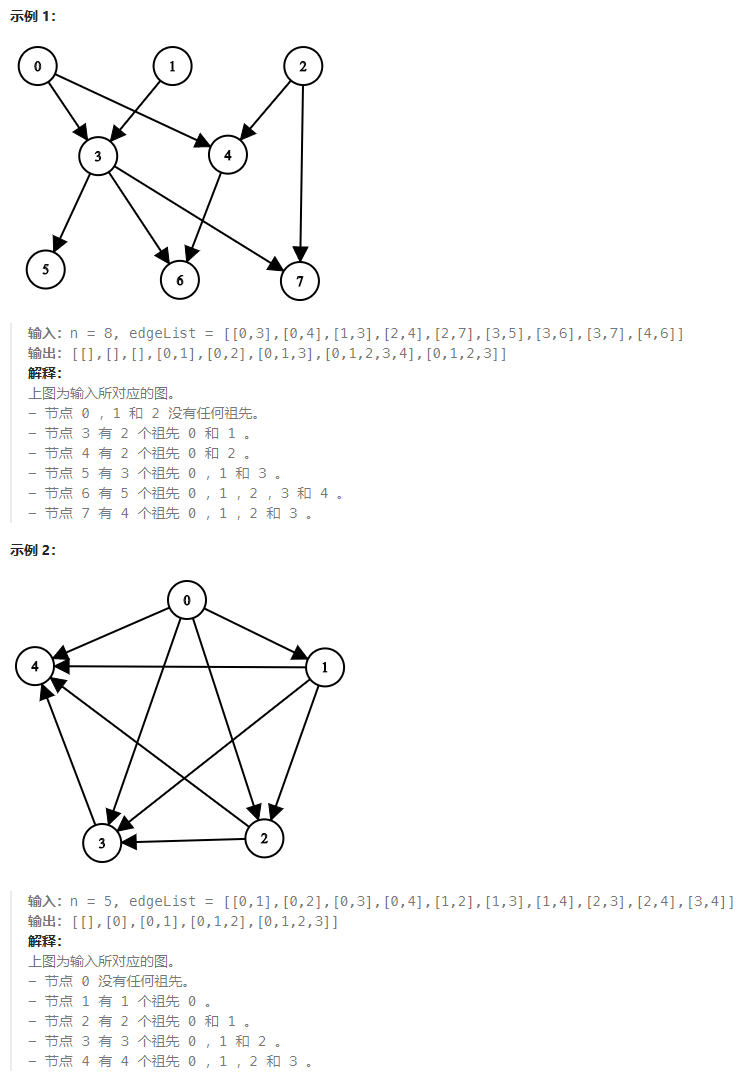
说明：

• 1 <= n <= 1000
• 0 <= edges.length <= min(2000, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi <= n - 1
• fromi != toi
• 图中不会有重边。
• 图是 有向 且 无环 的。

思路

这个题要求所有节点的祖先节点集合，最直接的想法就是广度遍历然后记录父节点，然后下一个节点的祖先节点就是其父节点加上父节点的祖先节点。

需要注意的点是图不一定连通，所以选定一个起点不一定能遍历到所有节点。如果直接将所有节点加入队列容易超时。解决方法是先找到没有父节点的根节点，然后再广度遍历。

如果节点已经在队列中就不需要重复放入队列了，因为该节点的祖先集合可以由队列中的节点一起更新。

代码

/**
 * @date 2024-04-04 21:49
 */
public class GetAncestors2192 {

    /** 先找出没有parent的节点放入队列，然后广度优先遍历即可*/
    public List<List<Integer>> getAncestors(int n, int[][] edges) {
        List<Integer>[] g = new ArrayList[n];
        Set<Integer>[] dp = new TreeSet[n];
        List<List<Integer>> res = new ArrayList<>(n);
        Deque<Integer> q = new ArrayDeque<>();
        boolean[] hasParent = new boolean[n];
        for (int i = 0; i < g.length; i++) {
            g[i] = new ArrayList<>();
            dp[i] = new TreeSet<>();
        }
        for (int[] edge : edges) {
            g[edge[0]].add(edge[1]);
            hasParent[edge[1]] = true;
        }
        for (int i = 0; i < hasParent.length; i++) {
            if (!hasParent[i]) {
                q.offer(i);
            }
        }
        while (!q.isEmpty()) {
            Integer from = q.poll();
            for (int i = 0; i < g[from].size(); i++) {
                dp[g[from].get(i)].addAll(dp[from]);
                dp[g[from].get(i)].add(from);
                if (!q.contains(g[from].get(i))) {
                    q.offer(g[from].get(i));
                }
            }
        }
        for (Set<Integer> integers : dp) {
            res.add(new ArrayList<>(integers));
        }
        return res;
    }
}

性能

勉强过关，官网还介绍了拓扑排序的方法，有机会再更新吧。