标签： 快速选择

1738.找出第K大的异或坐标值

目标

给你一个二维矩阵 matrix 和一个整数 k ，矩阵大小为 m x n 由非负整数组成。

矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j]（下标从 0 开始计数）执行异或运算得到。

请你找出 matrix 的所有坐标中第 k 大的值（k 的值从 1 开始计数）。

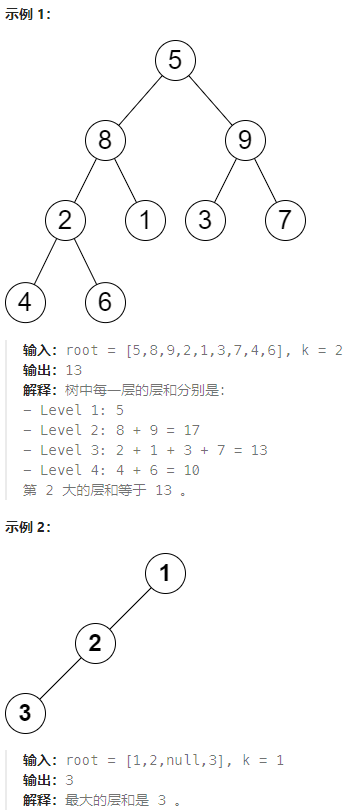
示例 1：

输入：matrix = [[5,2],[1,6]], k = 1
输出：7
解释：坐标 (0,1) 的值是 5 XOR 2 = 7 ，为最大的值。

示例 2：

输入：matrix = [[5,2],[1,6]], k = 2
输出：5
解释：坐标 (0,0) 的值是 5 = 5 ，为第 2 大的值。

示例 3：

输入：matrix = [[5,2],[1,6]], k = 3
输出：4
解释：坐标 (1,0) 的值是 5 XOR 1 = 4 ，为第 3 大的值。

示例 4：

输入：matrix = [[5,2],[1,6]], k = 4
输出：0
解释：坐标 (1,1) 的值是 5 XOR 2 XOR 1 XOR 6 = 0 ，为第 4 大的值。

说明：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 1000
  • 0 <= matrix[i][j] <= 10^6
  • 1 <= k <= m * n

思路

求二维矩阵 matrix 的第k大的异或坐标值，元素 matrix[i][j] 的异或坐标值等于对matrix[0][0] ~ matrix[i][j]矩阵中的所有值进行异或运算。

我们可以先分别对每一行按列进行异或运算，然后再针对每一列按行进行异或运算。然后将它们放入优先队列，再取第k大的值即可。

官网题解用到了二维前缀和 + 排序/快速选择。// todo

代码

/**
 * @date 2024-05-26 19:07
 */
public class KthLargestValue11738 {
    public int kthLargestValue(int[][] matrix, int k) {
        int m = matrix.length;
        int n = matrix[0].length;
        PriorityQueue<Integer> q = new PriorityQueue<>((a, b) -> b - a);
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            dp[i][0] = matrix[i][0];
        }
        for (int i = 0; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i][j - 1] ^ matrix[i][j];
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                dp[i][j] ^= dp[i - 1][j];
                q.offer(dp[i][j]);
            }
        }
        for (int i = 0; i < n; i++) {
            q.offer(dp[0][i]);
        }
        int res = 0;
        while (k > 0) {
            res = q.poll();
            k--;
        }

        return res;
    }
}

性能

2583.二叉树中的第K大层和

目标

给你一棵二叉树的根节点 root 和一个正整数 k 。

树中的 层和 是指 同一层 上节点值的总和。

返回树中第 k 大的 层和（不一定不同）。如果树少于 k 层，则返回 -1 。

注意，如果两个节点与根节点的距离相同，则认为它们在同一层。

说明：

  • 树中的节点数为 n
  • 2 <= n <= 10^5
  • 1 <= Node.val <= 10^6
  • 1 <= k <= n

思路

这个问题的关键在于遍历的同时记录层数并进行累加。由于是升序排列所以取倒数第k个，即MAX-k。

代码

/**
 * @date 2024-02-23 16:06
 */
public class KthLargestLevelSum {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

    public static void main(String[] args) {
        KthLargestLevelSum main = new KthLargestLevelSum();
        long res = main.kthLargestLevelSum(new TreeNode(1, new TreeNode(2), new TreeNode(3)), 2);
        System.out.println(res);
    }

    public final int MAX = 100000;
    public long[] lacc = new long[MAX];
    public int maxlevel = 0;

    public long kthLargestLevelSum(TreeNode root, int k) {
        traverseSubTree(root, 0);
        if (k > maxlevel + 1) {
            return -1;
        }
        Arrays.sort(lacc);
        return lacc[MAX-k];
    }
    public void traverseSubTree(TreeNode subTree, int level) {
        maxlevel = Math.max(maxlevel, level);
        lacc[level] += subTree.val;
        if (subTree.left != null) {
            traverseSubTree(subTree.left, level + 1);
        }
        if (subTree.right != null) {
            traverseSubTree(subTree.right, level + 1);
        }
    }
}

Arrays.sort使用的是双轴快排(DualPivotQuicksort)，时间复杂度是O(nlogn)。

性能

最优的算法是快速选择。因为我们并不需要所有的元素都有序，只要保证k位置的左侧都比k小，右侧均比k大即可，而两侧区间内部是不需要排序的。