目标
给你一个二维数组 edges 表示一个 n 个点的无向图,其中 edges[i] = [ui, vi, lengthi] 表示节点 ui 和节点 vi 之间有一条需要 lengthi 单位时间通过的无向边。
同时给你一个数组 disappear ,其中 disappear[i] 表示节点 i 从图中消失的时间点,在那一刻及以后,你无法再访问这个节点。
注意,图有可能一开始是不连通的,两个节点之间也可能有多条边。
请你返回数组 answer ,answer[i] 表示从节点 0 到节点 i 需要的 最少 单位时间。如果从节点 0 出发 无法 到达节点 i ,那么 answer[i] 为 -1 。
示例 1:
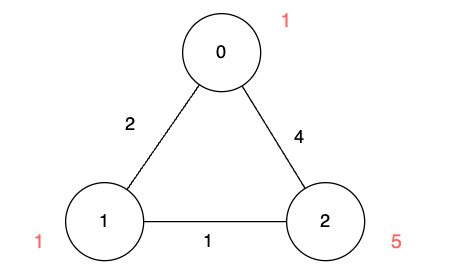
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]
输出:[0,-1,4]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。
对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
对于节点 1 ,我们需要至少 2 单位时间,通过 edges[0] 到达。但当我们到达的时候,它已经消失了,所以我们无法到达它。
对于节点 2 ,我们需要至少 4 单位时间,通过 edges[2] 到达。示例 2:
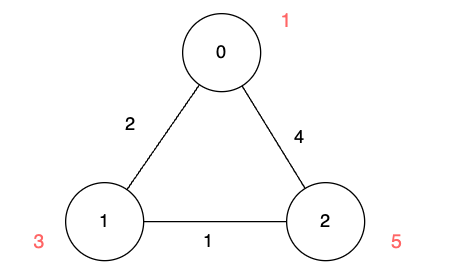
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]
输出:[0,2,3]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。
对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
对于节点 1 ,我们需要至少 2 单位时间,通过 edges[0] 到达。
对于节点 2 ,我们需要至少 3 单位时间,通过 edges[0] 和 edges[1] 到达。示例 3:
输入:n = 2, edges = [[0,1,1]], disappear = [1,1]
输出:[0,-1]
解释:
当我们到达节点 1 的时候,它恰好消失,所以我们无法到达节点 1 。说明:
- 1 <= n <= 5 * 10^4
- 0 <= edges.length <= 10^5
- edges[i] == [ui, vi, lengthi]
- 0 <= ui, vi <= n - 1
- 1 <= lengthi <= 10^5
- disappear.length == n
- 1 <= disappear[i] <= 10^5
思路
有一个n节点的带权无向图,权值表示经过该路径需要的时间。还有一个含有n个元素的数组,表示节点存在时间,即节点在该时间之后消失。让我们返回从0节点到达每个节点的最少时间,如到达时节点刚好消失则认为无法到达,返回-1。两节点之间可能有多条边,并且允许自己到自己的路径。
直接的想法是使用迪杰斯特拉算法求出到达各节点的最少时间,然后与节点消失时间比较。但是最短路径可能随着节点消失而变得不可达,因此需要在遍历的时候判断节点是否消失。
又重新手写了一遍,纠正了以前的误区:
- 对于距离dis初始化为INF的判断,认为INF+cost可能溢出。这是完全没有必要的,当前节点的dis一定已经更新过了。
- 容易写成dfs,每次都取当前节点邻居中最小的。但这样求得的可能不是最短路径。关于最短路径问题:
- 不带权,bfs
- 非负权,dijkstra
- 有负权,bellman-ford
- 多源(寻找图中所有顶点对之间最短路径)Floyd, 属于动态规划算法
- dijkstra 适用于DAG,对于无向图,需要避免环,或者向反方向查找。dijkstra类似于bfs,不过是取所有已访问节点的相邻节点中最小的,对于已处理的节点没有前往该节点更短的路径。
- dijkstra 算法的核心在于其选择下一个扩展顶点的策略和路径长度的累计方式,这与动态规划直接填充整个解决方案空间的策略有所不同。
- dijkstra 算法不依赖于特定的数据结构来选择最小节点,而是依赖算法本身的逻辑,不使用堆优化的实现依然可以得到正确的结果,只不过进行了不必要的计算。
代码
/**
* @date 2024-07-18 0:20
*/
public class MinimumTime3112 {
public int[] minimumTime(int n, int[][] edges, int[] disappear) {
List<int[]>[] g = new ArrayList[n];
for (int[] edge : edges) {
if (g[edge[0]] == null) {
g[edge[0]] = new ArrayList<>();
}
if (g[edge[1]] == null) {
g[edge[1]] = new ArrayList<>();
}
g[edge[0]].add(new int[]{edge[1], edge[2]});
g[edge[1]].add(new int[]{edge[0], edge[2]});
}
int[] dis = new int[n];
dis[0] = 0;
for (int i = 1; i < n; i++) {
dis[i] = Integer.MAX_VALUE;
}
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[1] - b[1]);
q.offer(new int[]{0, 0});
while (!q.isEmpty()) {
int[] node = q.poll();
int cur = node[0];
if (g[cur] == null || node[1] > dis[cur]){
continue;
}
for (int[] item : g[cur]) {
int next = item[0];
if (next == cur){
continue;
}
int cost = item[1];
int totalCost = dis[cur] + cost;
if (dis[next] <= totalCost || (cur != 0 && disappear[cur] <= dis[cur])) {
continue;
}
if (totalCost < disappear[next]) {
dis[next] = totalCost;
q.offer(new int[]{next, totalCost});
}
}
}
for (int i = 0; i < n; i++) {
if (dis[i] >= disappear[i]) {
dis[i] = -1;
}
}
return dis;
}
}
性能
将PriorityQueue改为LinkedList,不使用堆优化的反而更快,这就是测试用例的问题了。