目标
给出了一个由 n 个节点组成的网络,用 n × n 个邻接矩阵图 graph 表示。在节点网络中,当 graph[i][j] = 1 时,表示节点 i 能够直接连接到另一个节点 j。
一些节点 initial 最初被恶意软件感染。只要两个节点直接连接,且其中至少一个节点受到恶意软件的感染,那么两个节点都将被恶意软件感染。这种恶意软件的传播将继续,直到没有更多的节点可以被这种方式感染。
假设 M(initial) 是在恶意软件停止传播之后,整个网络中感染恶意软件的最终节点数。
如果从 initial 中移除某一节点能够最小化 M(initial), 返回该节点。如果有多个节点满足条件,就返回索引最小的节点。
请注意,如果某个节点已从受感染节点的列表 initial 中删除,它以后仍有可能因恶意软件传播而受到感染。
示例 1:
输入:graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1]
输出:0示例 2:
输入:graph = [[1,0,0],[0,1,0],[0,0,1]], initial = [0,2]
输出:0示例 3:
输入:graph = [[1,1,1],[1,1,1],[1,1,1]], initial = [1,2]
输出:1说明:
- n == graph.length
- n == graph[i].length
- 2 <= n <= 300
graph[i][j] == 0或 1.graph[i][j] == graph[j][i]graph[i][i] == 1- 1 <= initial.length <= n
- 0 <= initial[i] <= n - 1
- initial 中所有整数均不重复
思路
从 初始 已感染恶意软件的节点集合中去掉一个节点使得整个网络的感染节点数量最小,返回这个节点。注意,从初始被感染的集合中去除,并不代表后续不会再被感染。如果还有与它连通的恶意节点,那么仍会被感染,最终计算感染节点时要算上。
因此,如果被感染节点是连通的,去掉任一感染节点后,总的感染节点数量不会改变。这时需要将索引最小的节点返回。
刚开始的想法是先排除相互的连通的感染节点,然后取剩余节点中连接节点个数最多的那个。
这个想法没错,但是具体实现的时候,仅仅判断直接相连的两个节点是否同时在感染列表显然是不对的,因为存在间接连接的情况。并且直接从感染集合移除还好影响后续其它节点的判断。
于是想到了使用并查集。
官网的解法类似,将连通的节点染成同一颜色,然后在感染节点中看是否有颜色唯一的节点,即该连通区域中只有一个感染节点,然后找出连通区域节点数最大的,如果有多个颜色唯一节点,返回下标最小的。如果没有颜色唯一的节点,那么移除任一感染节点,总的感染数都不会减少,直接取下标最小的即可。
判断区域是否连通可以使用并查集,也可以使用深度优先搜索。
代码
/**
* @date 2024-04-16 8:29
*/
public class MinMalwareSpread924 {
public int[] u;
TreeSet<Integer> s;
HashSet<Integer> d = new HashSet<>();
public void merge(int x, int y) {
HashSet<Integer> tmp = new HashSet<>();
int rx = find(x, tmp);
int ry = find(y, tmp);
d.addAll(tmp);
if (s.contains(rx) && s.contains(ry)) {
if (rx > ry) {
u[rx] = ry;
} else if (rx < ry) {
u[ry] = rx;
}
} else if (s.contains(ry)) {
u[rx] = ry;
} else {
u[ry] = rx;
}
}
public int find(int x, HashSet<Integer> tmp) {
if (x != u[x]) {
if (s.contains(x) && s.contains(u[x])) {
tmp.add(x);
tmp.add(u[x]);
}
x = find(u[x], tmp);
}
return u[x];
}
public int find(int x) {
if (x != u[x]) {
x = find(u[x]);
}
return u[x];
}
public int count(int x) {
int cnt = 0;
int rt = find(x);
for (int i = 0; i < u.length; i++) {
if (rt == find(i)) {
cnt++;
}
}
return cnt;
}
public int minMalwareSpread(int[][] graph, int[] initial) {
int n = graph.length;
List<Integer>[] g = new ArrayList[n];
u = new int[n];
for (int i = 0; i < n; i++) {
g[i] = new ArrayList<>(n);
u[i] = i;
}
s = new TreeSet<>();
for (int i : initial) {
s.add(i);
}
int res = s.first();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (graph[i][j] == 1) {
g[i].add(j);
merge(i, j);
}
}
}
if (s.size() == d.size()) {
return res;
}
TreeSet<Integer> ini = new TreeSet<>((x, y) -> count(y) - count(x) == 0 ? x - y : count(y) - count(x));
for (int i : initial) {
if (!d.contains(i)) {
ini.add(i);
}
}
return ini.first();
}
}
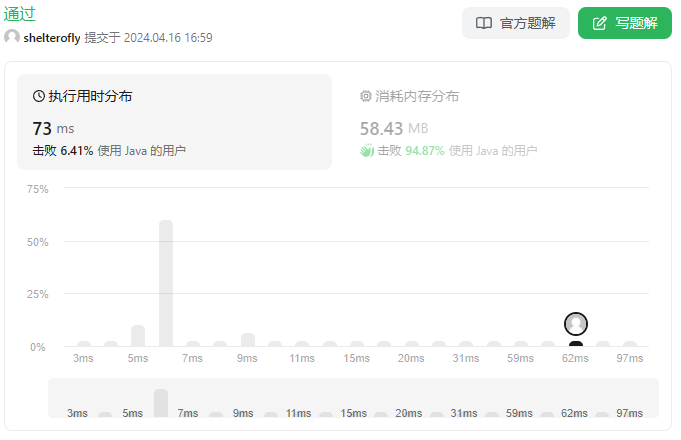
性能