目标
象棋骑士有一个独特的移动方式,它可以垂直移动两个方格,水平移动一个方格,或者水平移动两个方格,垂直移动一个方格(两者都形成一个 L 的形状)。
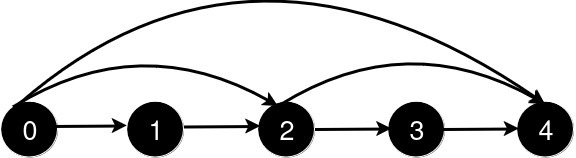
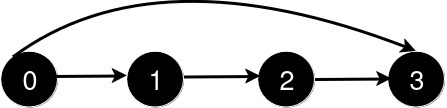
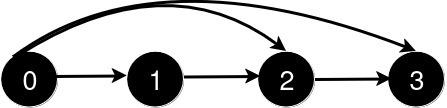
象棋骑士可能的移动方式如下图所示:

我们有一个象棋骑士和一个电话垫,如下所示,骑士只能站在一个数字单元格上(即蓝色单元格)。
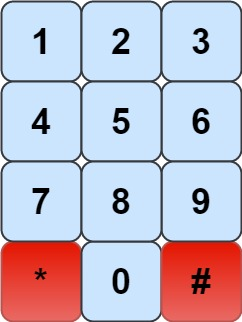
给定一个整数 n,返回我们可以拨多少个长度为 n 的不同电话号码。
你可以将骑士放置在任何数字单元格上,然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。
因为答案可能很大,所以输出答案模 10^9 + 7.
示例 1:
输入:n = 1
输出:10
解释:我们需要拨一个长度为1的数字,所以把骑士放在10个单元格中的任何一个数字单元格上都能满足条件。
示例 2:
输入:n = 2
输出:20
解释:我们可以拨打的所有有效号码为[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
示例 3:
输入:n = 3131
输出:136006598
解释:注意取模
说明:
思路
有一个电话键盘,布局如下:
1 2 3
4 5 6
7 8 9
* 0 #
开始时,将一个骑士棋子放在数字键上,然后按照国际象棋骑士的走法(类似于中国象棋里的马)走 n - 1 步,问能够组成多少种长度为 n 的不同号码(不能走到 * 和 #)。
这道题与 688.骑士在棋盘上的概率 类似,只不过棋盘更小,状态转移是确定的。
定义 dp[k][i] 表示以 i 结尾长度为 k 的号码组合数。初始时,dp[1][i] 均为 1。状态转移方程,针对不同的数字有所不同,例如 dp[k][1] = dp[k - 1][8] + dp[k - 1][6],dp[k][4] = dp[k - 1][3] + dp[k - 1][9] + dp[k - 1][0]等等。
1 - 6 - 7
| | |
8 0 2
| | |
3 - 4 - 9
仔细分析可以得到上面的状态转化图,1 3 7 9 的结果是完全相同的,同理 2 8 也可以认为是一个状态,4 6 是一个状态,0 是一个状态。定义以上 4 个状态为 a b c d,那么最终结果可以表示为 4 * dp[n][a] + 2 * dp[n][b] + 2 * dp[n][c] + dp[n][d],状态转移方程为:
dp[k][a] = dp[k - 1][b] + dp[k - 1][c]dp[k][b] = 2 * dp[k - 1][a]dp[k][c] = 2 * dp[k - 1][a] + dp[k - 1][d]dp[k][d] = 2 * dp[k - 1][c]
注意 k 的初值为 2,k == 1 是特殊情况,骑士可以在数字 5,但是无法继续移动。dp[2][a] = 2, dp[2][b] = 2, dp[2][c] = 3, dp[2][d] = 2
如果写成矩阵的形式 列向量 dp[k] 等于 A · dp[k - 1],其中矩阵 A 为:
0 1 1 0
2 0 0 0
2 0 0 1
0 0 2 0
因此 dp[n] = A^(n - 1) · dp[1],其中 dp[1] = [1, 1, 1, 1]。我们可以使用矩阵的快速幂求解。
代码
/**
* @date 2024-12-10 9:39
*/
public class KnightDialer935 {
public static int mod = 1000000007;
public int knightDialer_v3(int n) {
if (n == 1) {
return 10;
}
long[][] A = new long[][]{
{0, 1, 1, 0},
{2, 0, 0, 0},
{2, 0, 0, 1},
{0, 0, 2, 0},
};
A = pow(A, n - 1);
long[] res = new long[4];
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
res[i] += A[i][j];
}
}
return (int) ((4 * res[0] + 2 * res[1] + 2 * res[2] + res[3]) % mod);
}
public long[][] pow(long[][] A, int exponent) {
long[][] res = new long[][]{
{1, 0, 0, 0},
{0, 1, 0, 0},
{0, 0, 1, 0},
{0, 0, 0, 1},
};
while (exponent > 0) {
if ((exponent & 1) == 1) {
res = mul(A, res);
}
A = mul(A, A);
exponent >>= 1;
}
return res;
}
public long[][] mul(long[][] A1, long[][] A2) {
long[][] res = new long[4][4];
for (int i = 0; i < 4; i++) {
for (int k = 0; k < 4; k++) {
if (A1[i][k] == 0) {
continue;
}
for (int j = 0; j < 4; j++) {
res[i][j] = (res[i][j] + A1[i][k] * A2[k][j]) % mod;
}
}
}
return res;
}
public static long[][] dp;
public static int MAX = 5001;
static {
dp = new long[MAX][4];
dp[2][0] = 2;
dp[2][1] = 2;
dp[2][2] = 3;
dp[2][3] = 2;
for (int k = 3; k < MAX; k++) {
dp[k][0] = (dp[k - 1][1] + dp[k - 1][2]) % mod;
dp[k][1] = (2 * dp[k - 1][0]) % mod;
dp[k][2] = (2 * dp[k - 1][0] + dp[k - 1][3]) % mod;
dp[k][3] = (2 * dp[k - 1][2]) % mod;
}
}
public int knightDialer_v2(int n) {
if (n == 1) {
return 10;
}
return (int)((4 * dp[n][0] + 2 * dp[n][1] + 2 * dp[n][2] + dp[n][3]) % mod);
}
public int knightDialer_v1(int n) {
long[][] dp = new long[n + 1][10];
dp[1] = new long[]{1, 1, 1, 1, 1, 1, 1, 1, 1, 1};
int MOD = 1000000007;
int res = 0;
for (int k = 2; k <= n; k++) {
dp[k][0] = (dp[k - 1][4] + dp[k - 1][6]) % MOD;
dp[k][1] = (dp[k - 1][6] + dp[k - 1][8]) % MOD;
dp[k][2] = (dp[k - 1][7] + dp[k - 1][9]) % MOD;
dp[k][3] = (dp[k - 1][4] + dp[k - 1][8]) % MOD;
dp[k][4] = (dp[k - 1][3] + dp[k - 1][9] + dp[k - 1][0]) % MOD;
dp[k][6] = (dp[k - 1][1] + dp[k - 1][7] + dp[k - 1][0]) % MOD;
dp[k][7] = (dp[k - 1][2] + dp[k - 1][6]) % MOD;
dp[k][8] = (dp[k - 1][1] + dp[k - 1][3]) % MOD;
dp[k][9] = (dp[k - 1][2] + dp[k - 1][4]) % MOD;
}
for (int i = 0; i < 10; i++) {
res = (int) (res + dp[n][i]) % MOD;
}
return res;
}
}
性能