目标
给你一个整数数组 nums,请你找出并返回能被三整除的元素 最大和。
示例 1:
输入:nums = [3,6,5,1,8]
输出:18
解释:选出数字 3, 6, 1 和 8,它们的和是 18(可被 3 整除的最大和)。示例 2:
输入:nums = [4]
输出:0
解释:4 不能被 3 整除,所以无法选出数字,返回 0。示例 3:
输入:nums = [1,2,3,4,4]
输出:12
解释:选出数字 1, 3, 4 以及 4,它们的和是 12(可被 3 整除的最大和)。说明:
- 1 <= nums.length <= 4 * 10^4
- 1 <= nums[i] <= 10^4
思路
求整数数组中元素的最大和,要求和能被 3 整除。
- 如果和 sum % 3 == 1,可以去掉一个模 3 余 1 的最小元素,或者 两个模 3 余 2 的最小元素
- 如果和 sum % 3 == 2,可以去掉一个模 3 余 2 的最小元素,或者 两个模 3 余 1 的最小元素
代码
/**
* @date 2025-11-23 20:46
*/
public class MaxSumDivThree1262 {
public int maxSumDivThree(int[] nums) {
int res = 0;
PriorityQueue<Integer> q1 = new PriorityQueue<>();
PriorityQueue<Integer> q2 = new PriorityQueue<>();
for (int num : nums) {
res += num;
if (num % 3 == 1) {
q1.offer(num);
} else if (num % 3 == 2) {
q2.offer(num);
}
}
int mod = res % 3;
if (mod == 1) {
int sub = q1.size() == 0 ? 100000 : q1.peek();
if (q2.size() > 1) {
sub = Math.min(sub, q2.poll() + q2.poll());
}
res -= sub;
} else if (mod == 2) {
int sub = q2.size() == 0 ? 100000 : q2.peek();
if (q1.size() > 1) {
sub = Math.min(sub, q1.poll() + q1.poll());
}
res -= sub;
}
return res;
}
}
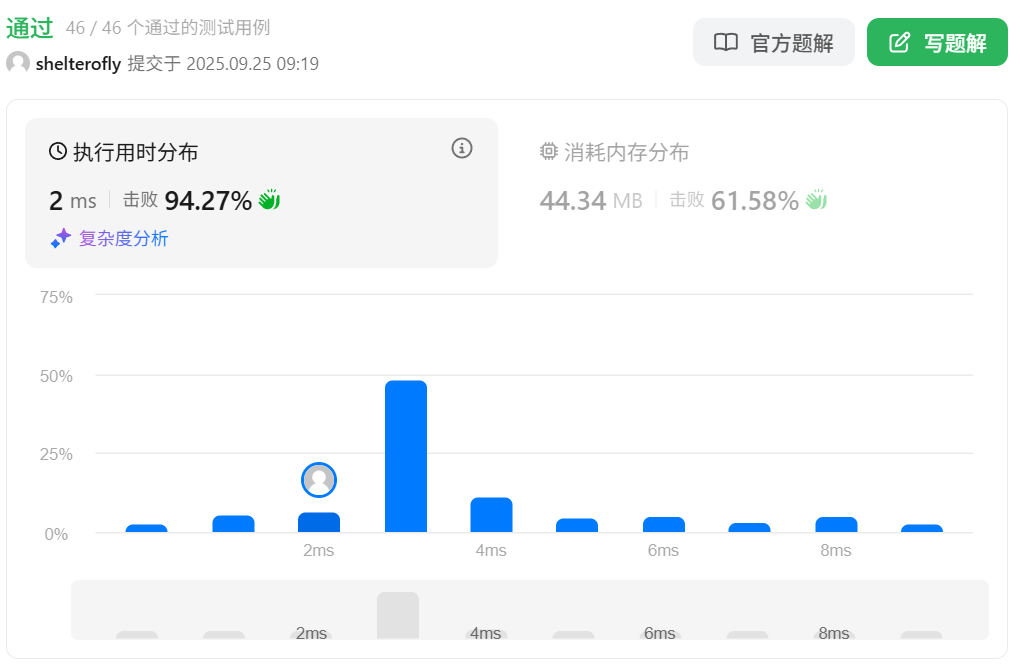
性能