标签： 动态规划

目标

给定一个长度为 n 的整数数组 nums 。

假设 arrk 是数组 nums 顺时针旋转 k 个位置后的数组，我们定义 nums 的 旋转函数 F 为：

• F(k) = 0 * arrk[0] + 1 * arrk[1] + ... + (n - 1) * arrk[n - 1]

返回 F(0), F(1), ..., F(n-1)中的最大值 。

生成的测试用例让答案符合 32 位 整数。

示例 1:

输入: nums = [4,3,2,6]
输出: 26
解释:
F(0) = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6) = 0 + 3 + 4 + 18 = 25
F(1) = (0 * 6) + (1 * 4) + (2 * 3) + (3 * 2) = 0 + 4 + 6 + 6 = 16
F(2) = (0 * 2) + (1 * 6) + (2 * 4) + (3 * 3) = 0 + 6 + 8 + 9 = 23
F(3) = (0 * 3) + (1 * 2) + (2 * 6) + (3 * 4) = 0 + 2 + 12 + 12 = 26
所以 F(0), F(1), F(2), F(3) 中的最大值是 F(3) = 26 。

示例 2:

输入: nums = [100]
输出: 0

说明:

• n == nums.length
• 1 <= n <= 10^5
• -100 <= nums[i] <= 100

思路

有一个循环数组 nums，arr_k 表示将数组 nums 循环右移 k 之后的数组。定义 F(k) = 0 * arr_k[0] + 1 * arr_k[1] + …… + (n - 1) * arr_k[n - 1]，返回 F(0)、F(1)、……、F(n - 1) 的最大值。

F(k) = Σ(i * arr_k[i])，观察发现 F(k + 1) - F(k) = sum - n * arr_k[n - 1]，其中 sum 是 nums 所有元素和。从 F(k) -> F(k + 1)，除了最后一个元素，所有元素都增加了一个，最后一个元素减少了 n - 1 个。这里前面多加了最后一个元素，所以后面减去 n 个。arr_k 的最后一个元素为 nums[n - k]。

代码

/**
 * @date 2026-05-09 13:43
 */
public class MaxRotateFunction396 {

    public int maxRotateFunction(int[] nums) {
        int n = nums.length;
        int f = 0;
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum += nums[i];
            f += i * nums[i];
        }
        int res = f;
        for (int i = 1; i < n; i++) {
            f += sum - n * nums[n - i];
            res = Math.max(res, f);
        }
        return res;
    }
}

性能

时间复杂度为 O(n)。

目标

给你一个 m x n 的网格 grid，其中每个单元格包含以下值之一：0、1 或 2。另给你一个整数 k。

你从左上角 (0, 0) 出发，目标是到达右下角 (m - 1, n - 1)，只能向 右 或 下 移动。

每个单元格根据其值对路径有以下贡献：

• 值为 0 的单元格：分数增加 0，花费 0。
• 值为 1 的单元格：分数增加 1，花费 1。
• 值为 2 的单元格：分数增加 2，花费 1。

返回在总花费不超过 k 的情况下可以获得的 最大分数 ，如果不存在有效路径，则返回 -1。

注意： 如果到达最后一个单元格时总花费超过 k，则该路径无效。

示例 1：

输入： grid = [[0, 1],[2, 0]], k = 1
输出： 2
解释：
最佳路径为：
单元格  grid[i][j] 当前分数 累计分数 当前花费 累计花费
(0, 0)     0         0      0        0       0
(1, 0)     2         2      2        1       1
(1, 1)     0         0      2        0       1
因此，可获得的最大分数为 2。

示例 2：

输入： grid = [[0, 1],[1, 2]], k = 1
输出： -1
解释：
不存在在总花费不超过 k 的情况下到达单元格 (1, 1) 的路径，因此答案是 -1。

说明：

• 1 <= m, n <= 200
• 0 <= k <= 10^3
• grid[0][0] == 0
• 0 <= grid[i][j] <= 2

思路

有一个 m x n 网格 grid，其元素值可取 0、1、2，从左上角 (0, 0) 移动到 (m - 1, n - )，每次移动只能向右或向下，移动的代价为 grid[i][j] == 0 ? 0 : 1。求总代价不超过 k 的条件下，从左上移动到右下的最大得分，如果不存在有效路径返回 -1。

定义 dp[i + 1][j + 1][c] 表示到达坐标 (i, j) 且代价不超过 c - 1 的最大得分。状态转移方程为 dp[i + 1][j + 1][c] = Math.max(dp[i][j + 1][c + cost], dp[i + 1][j][c + cost]) + grid[i][j]，其中 cost = grid[i][j] == 0 ? 0 : -1。

可以进行空间优化，直接将第一个维度去掉，内层倒序遍历即可。

代码

/**
 * @date 2026-04-30 8:57
 */
public class MaxPathScore3742 {

    public int maxPathScore_v2(int[][] grid, int k) {
        int n = grid[0].length;
        int[][] dp = new int[n + 1][k + 2];
        for (int[] row : dp) {
            Arrays.fill(row, Integer.MIN_VALUE);
        }
        Arrays.fill(dp[1], 1, k + 2, 0);
        for (int[] row : grid) {
            for (int j = 0; j < n; j++) {
                int cost = row[j] == 0 ? 0 : -1;
                for (int c = k + 1; c >=1; c--) {
                    dp[j + 1][c] = Math.max(dp[j + 1][c + cost], dp[j][c + cost]) + row[j];
                }
            }
        }
        return dp[n][k + 1] < 0 ? -1 : dp[n][k + 1];
    }

}

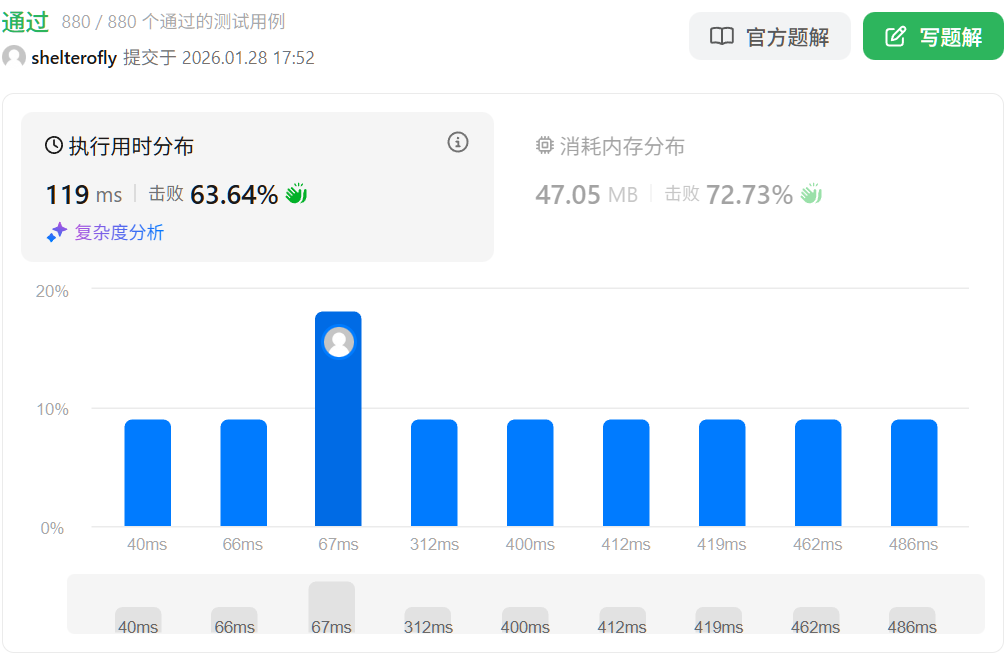
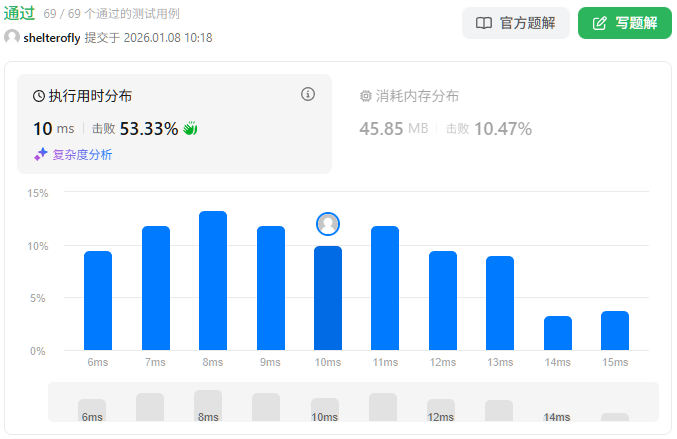
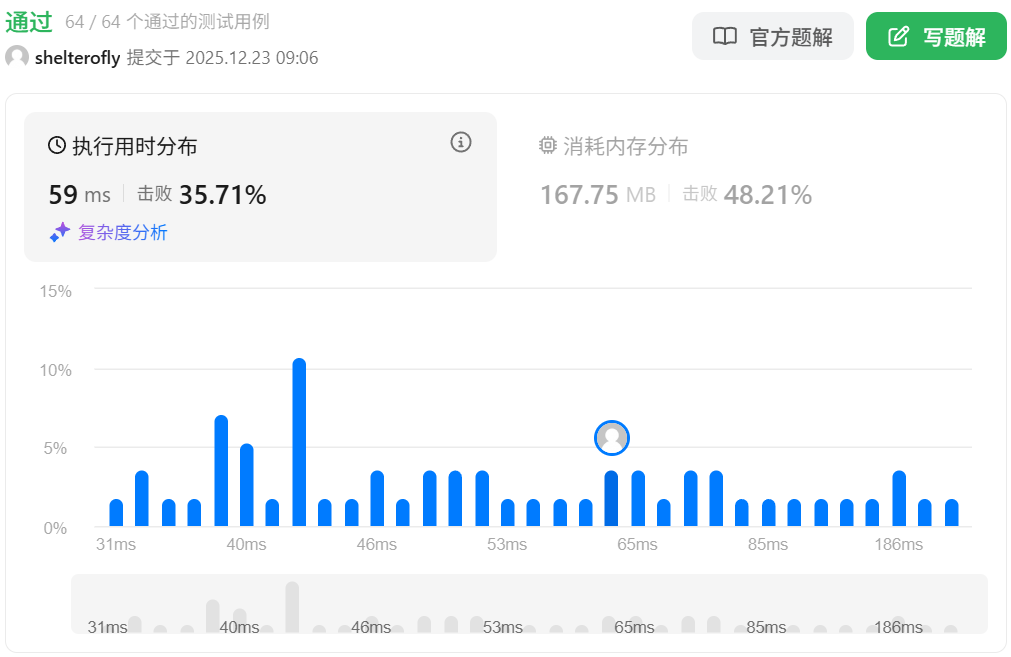
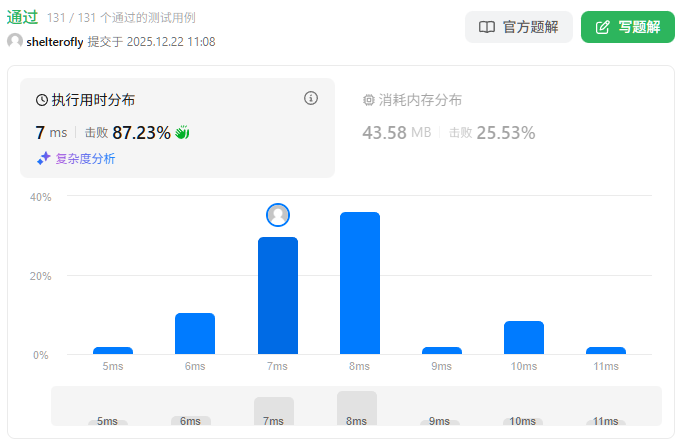
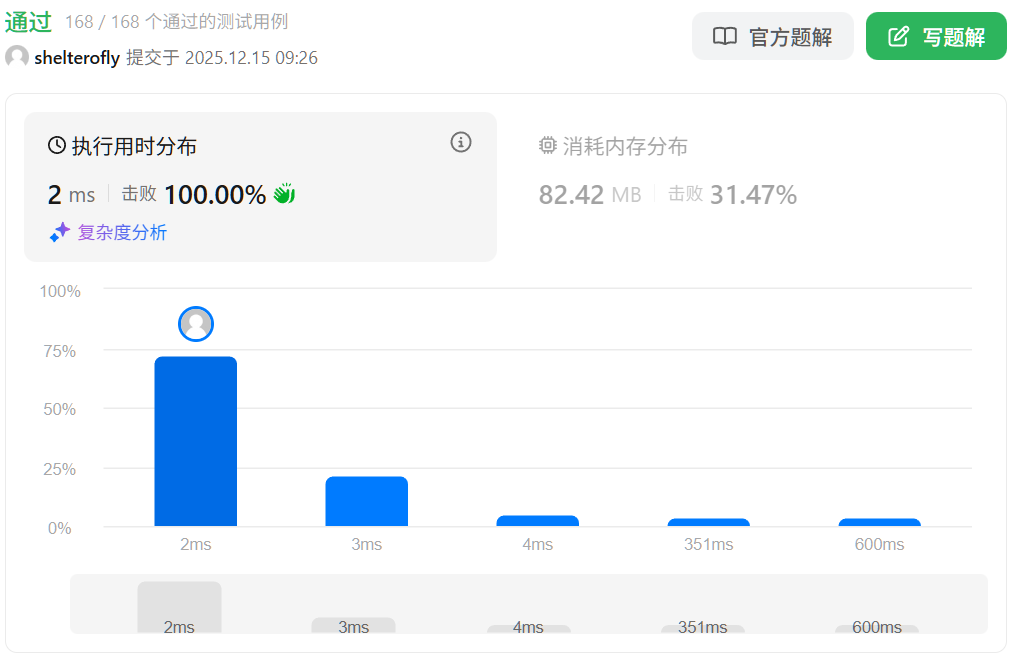
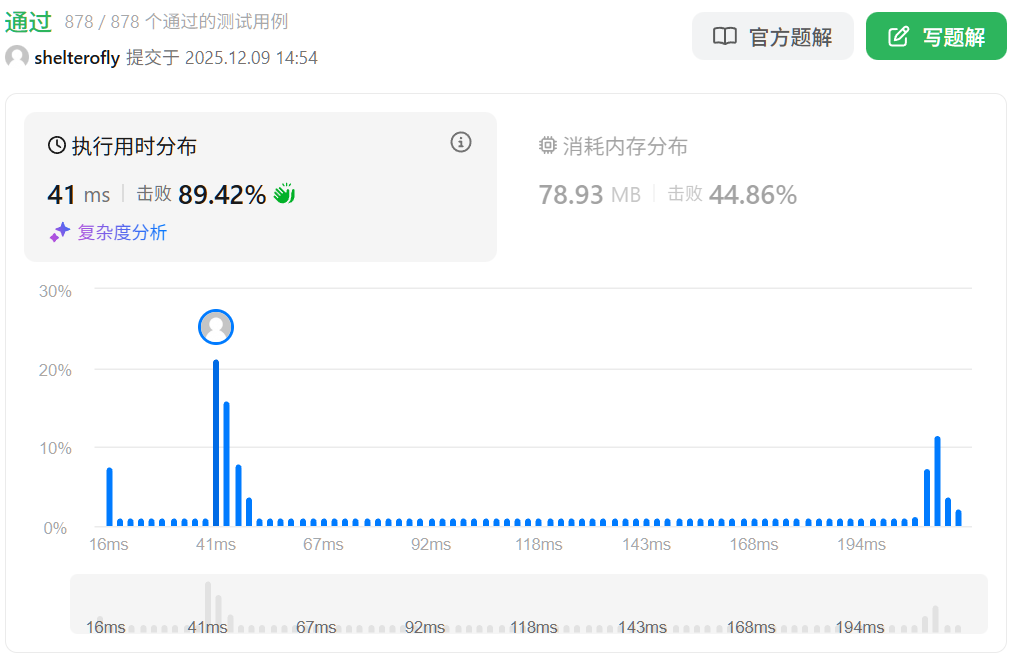
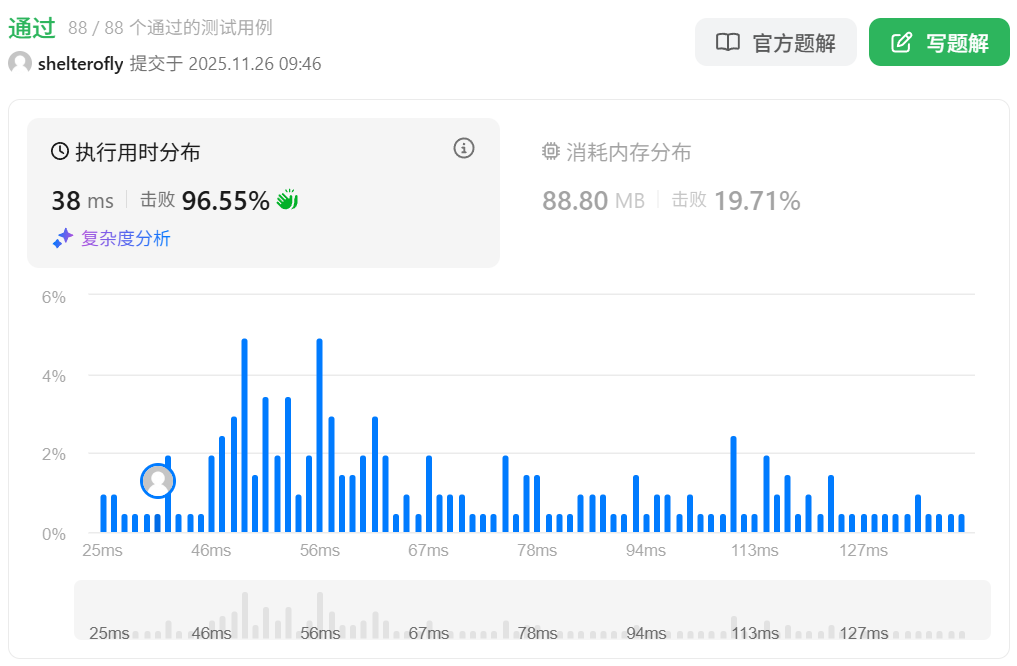
性能