目标
给你一个二维数组 points 和一个字符串 s ，其中 points[i] 表示第 i 个点的坐标，s[i] 表示第 i 个点的 标签 。
如果一个正方形的中心在 (0, 0) ，所有边都平行于坐标轴，且正方形内 不 存在标签相同的两个点，那么我们称这个正方形是 合法 的。
请你返回 合法 正方形中可以包含的 最多 点数。
注意：
- 如果一个点位于正方形的边上或者在边以内，则认为该点位于正方形内。
- 正方形的边长可以为零。
示例 1：
输入：points = [[2,2],[-1,-2],[-4,4],[-3,1],[3,-3]], s = "abdca"
输出：2
解释：边长为 4 的正方形包含两个点 points[0] 和 points[1] 。示例 2：
输入：points = [[1,1],[-2,-2],[-2,2]], s = "abb"
输出：1
解释：边长为 2 的正方形包含 1 个点 points[0] 。示例 3：
输入：points = [[1,1],[-1,-1],[2,-2]], s = "ccd"
输出：0
解释：任何正方形都无法只包含 points[0] 和 points[1] 中的一个点，所以合法正方形中都不包含任何点。说明：
- 1 <= s.length, points.length <= 10^5
- points[i].length == 2
-10^9 <= points[i][0], points[i][1] <= 10^9- s.length == points.length
- points 中的点坐标互不相同。
- s 只包含小写英文字母。
思路
坐标平面上有一些点points，每个点都有一个标签字母，points[i] 对应的标签为给定字符串s相应位置上的字母 s.charAt(i)。问以坐标轴原点为中心的正方形最多能覆盖多少标签不同的坐标点。
坐标平面内的点如果想要被以原点为中心的正方形覆盖，那么正方形的边长应大于等于max(|x|,|y|)，即切比雪夫距离。又要使坐标点的标签不同，可以将坐标点的 切比雪夫距离 从小到大排序，然后依次遍历并将其标签加入哈希表，直到遇到重复的为止。需要注意，应将该边长上的所有已经加入的坐标点删除，为此我们可以将距离相同的坐标放入一个集合，要么都计入，要么结束循环。
看了题解，网友还提供了两种解法，一个是使用二分法枚举边长范围，看正方形内是否有重复坐标；另一个是建立 字母 <---> 最小距离 的映射，同时计算最小的 次小距离，统计映射中的最小距离 小于 最小 次小距离 的坐标点个数即可。
代码
/**
* @date 2024-08-03 21:44
*/
public class MaxPointsInsideSquare3143 {
public int maxPointsInsideSquare(int[][] points, String s) {
int n = points.length;
Map<Integer, List<Integer>> map = new TreeMap<>();
for (int i = 0; i < n; i++) {
int key = Math.max(Math.abs(points[i][0]), Math.abs(points[i][1]));
map.putIfAbsent(key, new ArrayList<>());
map.get(key).add(i);
}
Set<Character> labelSet = new HashSet<>();
int res = 0;
here:
for (Map.Entry<Integer, List<Integer>> entry : map.entrySet()) {
for (Integer i : entry.getValue()) {
if (labelSet.contains(s.charAt(i))) {
break here;
}
labelSet.add(s.charAt(i));
}
res += entry.getValue().size();
}
return res;
}
}
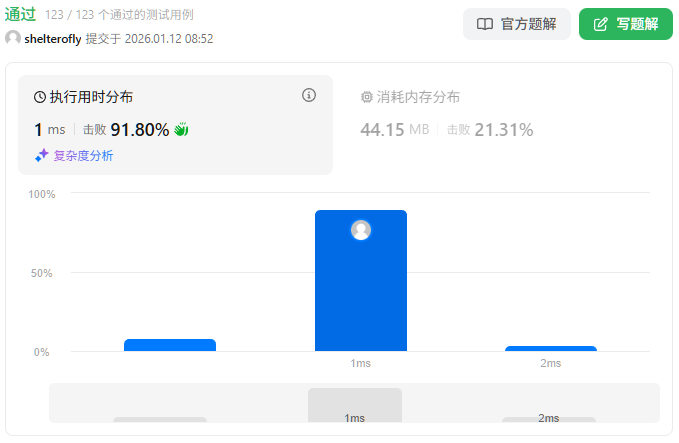
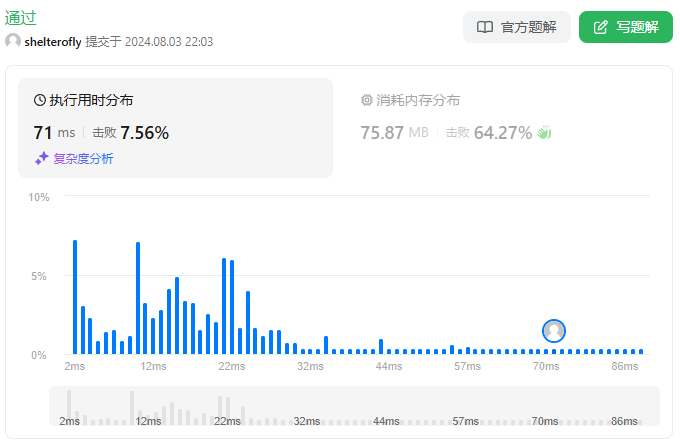
性能
