目标
给你两个长度分别为 n 和 m 的整数数组 skill 和 mana 。
在一个实验室里,有 n 个巫师,他们必须按顺序酿造 m 个药水。每个药水的法力值为 mana[j],并且每个药水 必须 依次通过 所有 巫师处理,才能完成酿造。第 i 个巫师在第 j 个药水上处理需要的时间为 timeij = skill[i] * mana[j]。
由于酿造过程非常精细,药水在当前巫师完成工作后 必须 立即传递给下一个巫师并开始处理。这意味着时间必须保持 同步,确保每个巫师在药水到达时 马上 开始工作。
返回酿造所有药水所需的 最短 总时间。
示例 1:
输入: skill = [1,5,2,4], mana = [5,1,4,2]
输出: 110
解释:
药水编号 开始时间 巫师 0 完成时间 巫师 1 完成时间 巫师 2 完成时间 巫师 3 完成时间
0 0 5 30 40 60
1 52 53 58 60 64
2 54 58 78 86 102
3 86 88 98 102 110
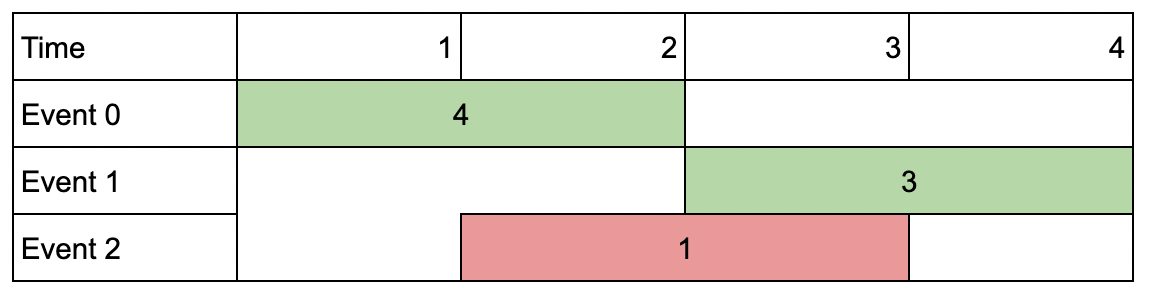
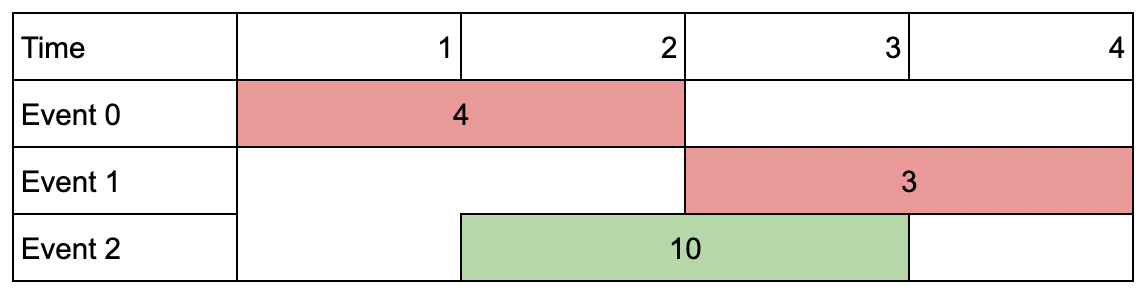
举个例子,为什么巫师 0 不能在时间 t = 52 前开始处理第 1 个药水,假设巫师们在时间 t = 50 开始准备第 1 个药水。时间 t = 58 时,巫师 2 已经完成了第 1 个药水的处理,但巫师 3 直到时间 t = 60 仍在处理第 0 个药水,无法马上开始处理第 1个药水。示例 2:
输入: skill = [1,1,1], mana = [1,1,1]
输出: 5
解释:
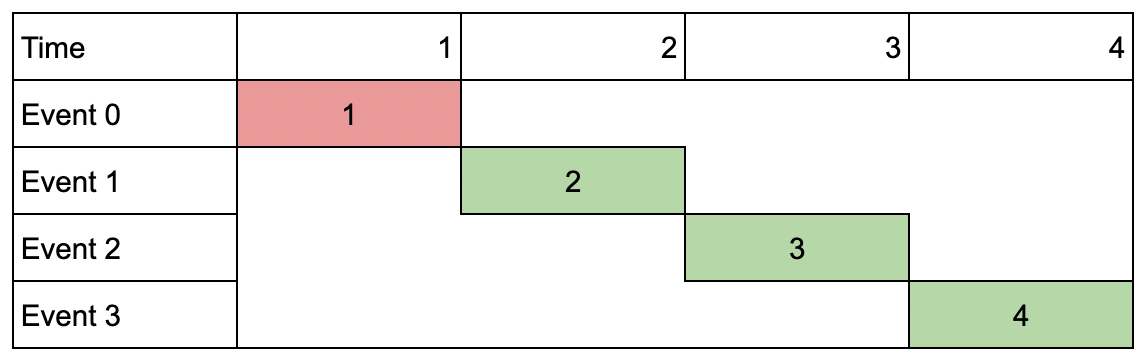
第 0 个药水的准备从时间 t = 0 开始,并在时间 t = 3 完成。
第 1 个药水的准备从时间 t = 1 开始,并在时间 t = 4 完成。
第 2 个药水的准备从时间 t = 2 开始,并在时间 t = 5 完成。示例 3:
输入: skill = [1,2,3,4], mana = [1,2]
输出: 21说明:
- n == skill.length
- m == mana.length
- 1 <= n, m <= 5000
- 1 <= mana[i], skill[i] <= 5000
思路
有 n 个巫师按顺序酿造 m 个药水,每个药水必须按顺序依次由 n 个巫师处理。第 i 个巫师处理第 j 个药水的时间为 skill[i] * mana[j]。求酿造所有药水所需的最短总时间。
定义 dp[i][j] 表示巫师 j - 1 制作完第 i - 1 瓶药的最短时间,状态转移方程为 dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]) + skill[j - 1] * mana[i - 1],即前面巫师的完成时间以及当前巫师上一轮的完成时间。当前药水完成之后需要倒序更新各个巫师的完成时间,因为状态转移方程只能保证最后一个巫师完成的时间是正确的,前面巫师的完成时间应该由最后一个完成时间来倒推。如果不更新会导致下一瓶药水的制作时间偏早。
// todo 学习其它题解
代码
/**
* @date 2025-10-09 9:02
*/
public class MinTime3494 {
public long minTime(int[] skill, int[] mana) {
int n = skill.length;
int m = mana.length;
long[][] dp = new long[m + 1][n + 2];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]) + skill[j - 1] * mana[i - 1];
}
for (int j = n - 1; j >= 1; j--) {
dp[i][j] = dp[i][j + 1] - skill[j] * mana[i - 1];
}
}
return dp[m][n];
}
}
性能