标签： 中序遍历

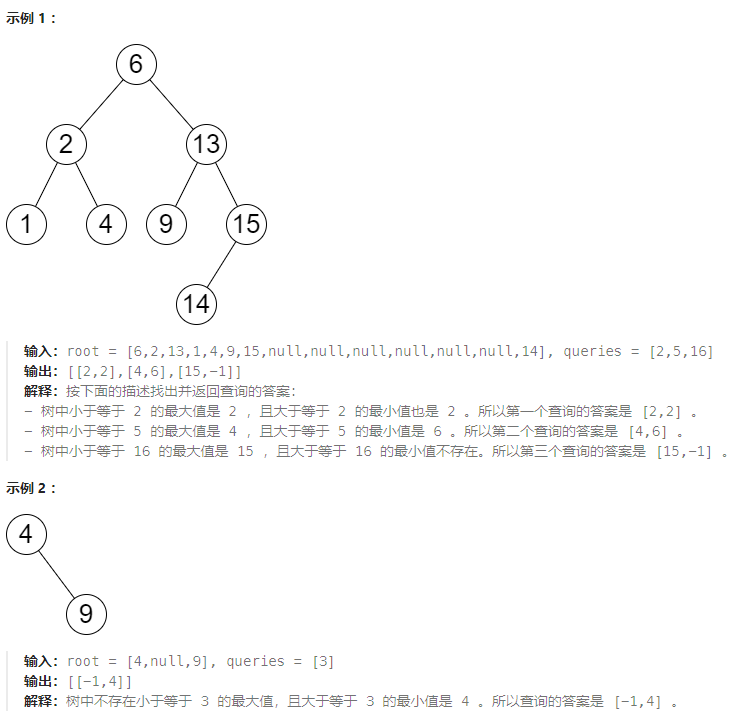
目标

给你一个 二叉搜索树 的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的 二维 答案数组 answer ，其中 answer[i] = [mini, maxi] ：

• mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值，则使用 -1 代替。
• maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值，则使用 -1 代替。

返回数组 answer 。

说明：

• 树中节点的数目在范围 [2, 10^5] 内
• 1 <= Node.val <= 10^6
• n == queries.length
• 1 <= n <= 10^5
• 1 <= queries[i] <= 10^6

思路

这个题目求的是最接近给定值的节点值。一个朴素的想法是将搜索树的值都列出来，然后从中查找前后的值。这里列出值无需保留树的结构，虽然节点数目范围是[2,10^5]，但如果考虑一个极端的情况，树的深度就是10^5-1，保留树的结构就大约需要2^(10^5)约等于10^3010个元素。二叉搜索树如果采用中序遍历结果就是正序的。但是考虑到存在null值，数组可能填不满，这样就破坏了有序性。想要使用二分查找还要先排序。Arrays.binarySearch 的结果如果找到相应的值则返回对应的index>=0。如果没有找到，则返回-insertion point-1。所谓插入点，其前一个位置的值小于搜索的值。例如 arr = [2, 3, 4, 5, 6, 7, 9] 搜索值为8，使用二分查找则返回 -6-1，arr[5]的值是7，8应该插入到7后面，即插入点为6。因此，如果没查询到，可以使用-index-1得到最近的大于搜索值的位置，这里需要注意数组的边界。

代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * @date 2024-02-24 18:57
 */
public class ClosestNodes {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

    public final int MAX = 100000;
    public int[] values = new int[MAX];
    public int i = 0;

    public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
        Arrays.fill(values, -1);
        traverseSubTree(root);
        // 遍历之后values并非全部有序，因为存在null节点，没初始化 值为0
        Arrays.sort(values);
        List<List<Integer>> res = new ArrayList<>(queries.size());
        for (Integer query : queries) {
            List<Integer> tmp = new ArrayList<>(2);
            int ri = Arrays.binarySearch(values, query);
            if (ri < 0) {
                ri = -ri - 1;
                if (ri == values.length) {
                    tmp.add(values[values.length -1]);
                    tmp.add(-1);
                } else if(ri == 0){
                    tmp.add(-1);
                    tmp.add(values[0]);
                } else {
                    tmp.add(values[ri - 1]);
                    tmp.add(values[ri]);
                }
            } else {
                // 如果存在
                tmp.add(values[ri]);
                tmp.add(values[ri]);
            }
            res.add(tmp);
        }
        return res;
    }

    public void traverseSubTree(TreeNode subTree) {
        if (subTree.left != null) {
            traverseSubTree(subTree.left);
        }
        values[i++] = subTree.val;
        if (subTree.right != null) {
            traverseSubTree(subTree.right);
        }
    }
}

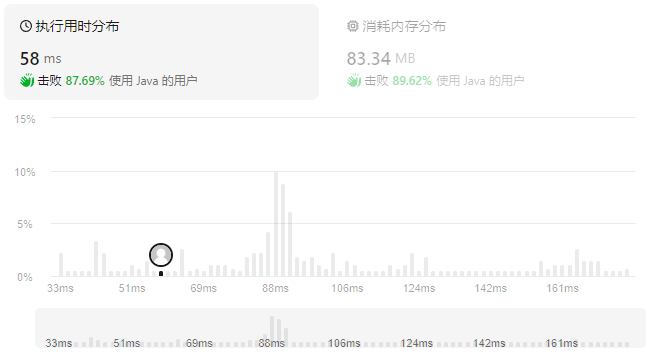
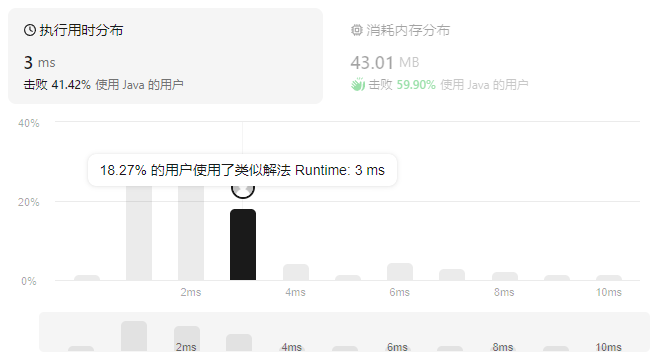
性能

目标

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

思路

有了前面 从前序与中序遍历序列构造二叉树 的经验这个问题就很好处理了。二叉树的后序遍历指先访问左子树、再访问右子树，最后访问根节点。

只需从后序序列的最后一个元素向前遍历即可，最后一个是根节点，接着是右子树、左子树的根节点 （注意这里是先右后左）。

还是在中序遍历中找到该根节点，然后其左侧的为左子树，右侧为右子树。依次递归遍历右子树与左子树，在递归方法中根节点取后序序列的前一个节点即可。

代码

/**
 * @date 2024-02-21 14:12
 */
public class BuildBinaryTreeFromMidPost {
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

//    static int[] inorder = new int[]{9, 3, 15, 20, 7};
    static int[] inorder = new int[]{2,3,1};
//    static int[] inorder = new int[]{-1};

//    static int[] postorder = new int[]{9, 15, 7, 20, 3};
    static int[] postorder = new int[]{3,2,1};
//    static int[] postorder = new int[]{-1};

    static int postCursor = postorder.length - 1;

    public static void main(String[] args) {
        int rootIndex = 0;
        TreeNode root = new TreeNode(postorder[postCursor]);
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == postorder[postCursor]) {
                rootIndex = i;
                // 一定能够找到
                postCursor--;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        // 注意这个postCursor应该是共享变量，原先是想以参数传递的，但是发现递归的时候还要将它传回来，改成了共享变量
        // 这里是先遍历右子树再左子树
        if (rightStartIndex < inorder.length) {
            root.right = traverseSubTree(inorder, rightStartIndex, inorder.length);
        }
        if (leftEndIndex >= 0) {
            root.left = traverseSubTree(inorder, 0, leftEndIndex);
        }
        System.out.println(root);
    }

    public static TreeNode traverseSubTree(int[] inorder, int start, int end) {
        TreeNode subRoot = new TreeNode(postorder[postCursor]);
        int rootIndex = start;
        for (int i = start; i <= end; i++) {
            if (inorder[i] == postorder[postCursor]) {
                rootIndex = i;
                postCursor--;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        // 临界条件判断，这里应该是<=，并且排除掉inorder.length
        // 这里是先遍历右子树再左子树
        if (rightStartIndex <= end && rightStartIndex != inorder.length) {
            // 这里的结束条件传end
            subRoot.right = traverseSubTree(inorder, rightStartIndex, end);
        }
        if (leftEndIndex >= start) {
            subRoot.left = traverseSubTree(inorder, start, leftEndIndex);
        }
        return subRoot;
    }
}

性能

目标

给定两个整数数组 preorder 和 inorder，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

思路

首先要明白先序遍历与中序遍历的概念。所谓二叉树的 先序遍历 指的是 先访问根节点，然后遍历左子树，再遍历右子树。中序遍历 则是 先遍历左子树，再根节点，然后右子树。

很容易想到使用递归，关键点是数组左右边界的维护，临界条件的判断。

注意到 先序遍历数组的第一个节点一定是根节点，其后面的节点则是其左子树或右子树的根节点。

于是先根据根节点在中序遍历中找到该根节点，然后其左侧的为左子树，右侧为右子树。依次递归遍历左子树与右子树（注意判断边界条件），在递归方法中根节点取刚才根节点的后一个节点（需要一个共享变量来记录位置）。

代码

/**
 * @date 2024-02-20 11:43
 */
public class BuildBinaryTree {

    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "val=" + val +
                    ", left=" + left +
                    ", right=" + right +
                    '}';
        }
    }

    static int[] preorder = new int[]{3, 9, 20, 15, 7};
//    static int[] preorder = new int[]{1,2,3};
//    static int[] preorder = new int[]{-1};

    static int[] inorder = new int[]{9, 3, 15, 20, 7};
//    static int[] inorder = new int[]{2,3,1};
//    static int[] inorder = new int[]{-1};

    static int preCursor = 0;

    public static void main(String[] args) {
        int rootIndex = 0;
        TreeNode root = new TreeNode(preorder[preCursor]);
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == preorder[preCursor]) {
                rootIndex = i;
                // 一定能够找到
                preCursor++;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        if (leftEndIndex >= 0) {
            root.left = traverseSubTree(inorder, 0, leftEndIndex);
        }
        // 注意这个preCursor应该是共享变量
        if (rightStartIndex < inorder.length) {
            root.right = traverseSubTree(inorder, rightStartIndex, inorder.length);
        }
        System.out.println(root);
    }

    public static TreeNode traverseSubTree(int[] inorder, int start, int end) {
        TreeNode subRoot = new TreeNode(preorder[preCursor]);
        int rootIndex = start;
        for (int i = start; i <= end; i++) {
            if (inorder[i] == preorder[preCursor]) {
                rootIndex = i;
                preCursor++;
                break;
            }
        }
        int leftEndIndex = rootIndex - 1;
        int rightStartIndex = rootIndex + 1;
        if (leftEndIndex >= start) {
            subRoot.left = traverseSubTree(inorder, start, leftEndIndex);
        }
        // 临界条件判断，这里应该是<=，并且排除掉inorder.length
        if (rightStartIndex <= end && rightStartIndex != inorder.length) {
            // 这里的结束条件传end
            subRoot.right = traverseSubTree(inorder, rightStartIndex, end);
        }
        return subRoot;
    }
}

性能

我的目标是能解决问题就好，看了下性能分布还有优化的空间，官网还给出了迭代的解法，没时间看。递归应该是更容易理解的方法了。希望能够坚持下去吧。