目标
一个任务管理器系统可以让用户管理他们的任务,每个任务有一个优先级。这个系统需要高效地处理添加、修改、执行和删除任务的操作。
请你设计一个 TaskManager 类:
TaskManager(vector<vector
void add(int userId, int taskId, int priority) 表示给用户 userId 添加一个优先级为 priority 的任务 taskId ,输入 保证 taskId 不在系统中。
void edit(int taskId, int newPriority) 更新已经存在的任务 taskId 的优先级为 newPriority 。输入 保证 taskId 存在于系统中。
void rmv(int taskId) 从系统中删除任务 taskId 。输入 保证 taskId 存在于系统中。
int execTop() 执行所有用户的任务中优先级 最高 的任务,如果有多个任务优先级相同且都为 最高 ,执行 taskId 最大的一个任务。执行完任务后,taskId 从系统中 删除 。同时请你返回这个任务所属的用户 userId 。如果不存在任何任务,返回 -1 。
注意 ,一个用户可能被安排多个任务。
示例 1:
输入:
["TaskManager", "add", "edit", "execTop", "rmv", "add", "execTop"]
[[[[1, 101, 10], [2, 102, 20], [3, 103, 15]]], [4, 104, 5], [102, 8], [], [101], [5, 105, 15], []]
输出:
[null, null, null, 3, null, null, 5]
解释:
TaskManager taskManager = new TaskManager([[1, 101, 10], [2, 102, 20], [3, 103, 15]]); // 分别给用户 1 ,2 和 3 初始化一个任务。
taskManager.add(4, 104, 5); // 给用户 4 添加优先级为 5 的任务 104 。
taskManager.edit(102, 8); // 更新任务 102 的优先级为 8 。
taskManager.execTop(); // 返回 3 。执行用户 3 的任务 103 。
taskManager.rmv(101); // 将系统中的任务 101 删除。
taskManager.add(5, 105, 15); // 给用户 5 添加优先级为 15 的任务 105 。
taskManager.execTop(); // 返回 5 。执行用户 5 的任务 105 。说明:
- 1 <= tasks.length <= 10^5
- 0 <= userId <= 10^5
- 0 <= taskId <= 10^5
- 0 <= priority <= 10^9
- 0 <= newPriority <= 10^9
- add ,edit ,rmv 和 execTop 的总操作次数 加起来 不超过 2 * 10^5 次。
- 输入保证 taskId 是合法的。
思路
与 2349.设计数字容器系统 类似,同样是懒删除。
代码
/**
* @date 2025-09-18 8:42
*/
public class TaskManager3408 {
static class TaskManager {
private final Map<Integer, int[]> taskIdMap = new HashMap<>();
private final PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> {
int compare = b[2] - a[2];
if (compare != 0) {
return compare;
}
return b[1] - a[1];
});
public TaskManager(List<List<Integer>> tasks) {
for (List<Integer> task : tasks) {
int[] t = {task.get(0), task.get(1), task.get(2)};
taskIdMap.put(t[1], t);
q.offer(t);
}
}
public void add(int userId, int taskId, int priority) {
int[] t = {userId, taskId, priority};
taskIdMap.put(taskId, t);
q.offer(t);
}
public void edit(int taskId, int newPriority) {
int[] t = taskIdMap.get(taskId);
t = new int[]{t[0], t[1], newPriority};
taskIdMap.put(taskId, t);
q.offer(t);
}
public void rmv(int taskId) {
taskIdMap.remove(taskId);
}
public int execTop() {
while (!q.isEmpty() && (taskIdMap.get(q.peek()[1]) == null || taskIdMap.get(q.peek()[1])[2] != q.peek()[2]|| taskIdMap.get(q.peek()[1])[0] != q.peek()[0])) {
q.poll();
}
if (q.isEmpty()) {
return -1;
}
int[] task = q.poll();
taskIdMap.remove(task[1]);
return task[0];
}
}
}
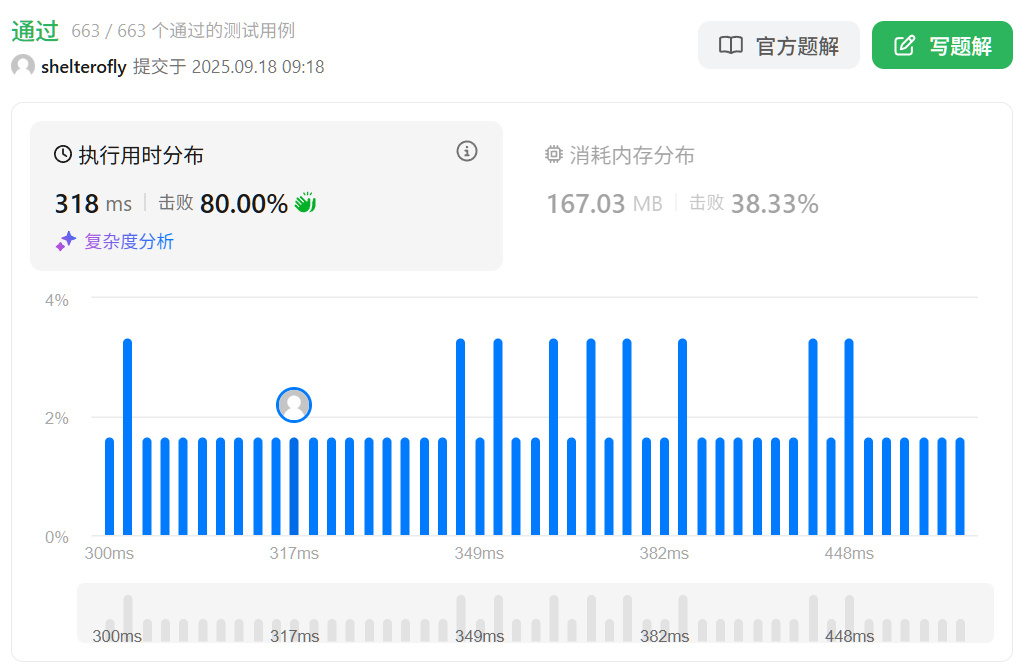
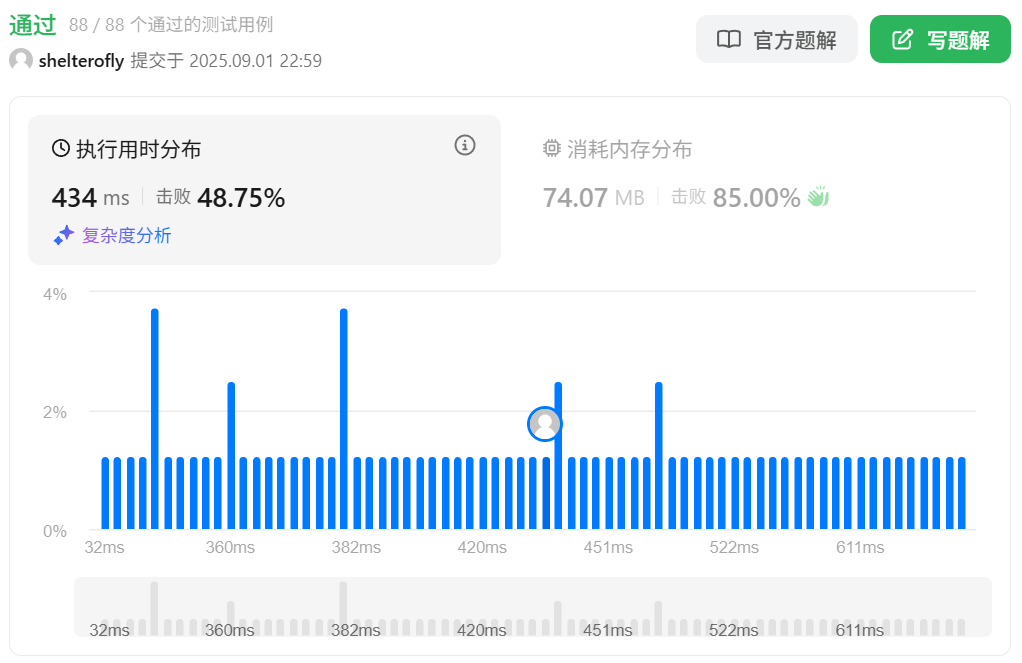
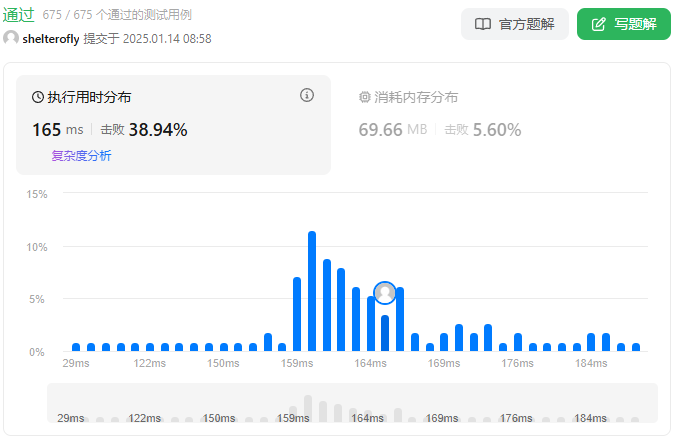
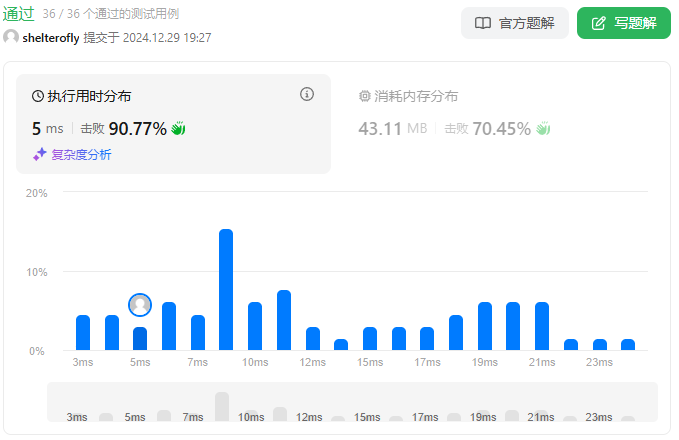
性能