目标
给你一棵二叉树,它的根为 root 。请你删除 1 条边,使二叉树分裂成两棵子树,且它们子树和的乘积尽可能大。
由于答案可能会很大,请你将结果对 10^9 + 7 取模后再返回。
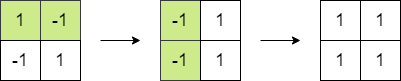
示例 1:
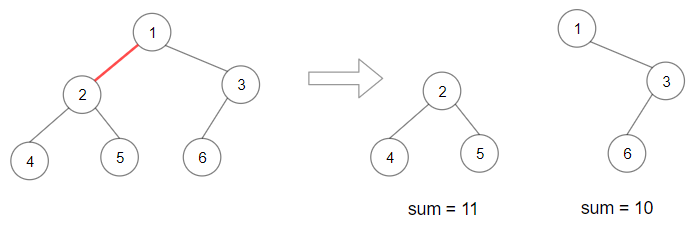
输入:root = [1,2,3,4,5,6]
输出:110
解释:删除红色的边,得到 2 棵子树,和分别为 11 和 10 。它们的乘积是 110 (11*10)
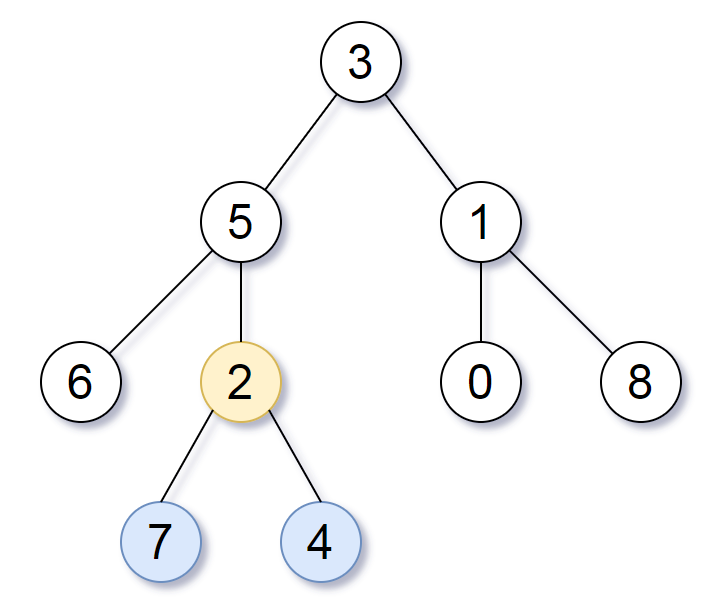
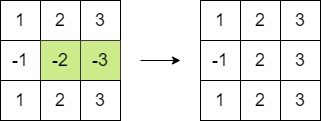
示例 2:
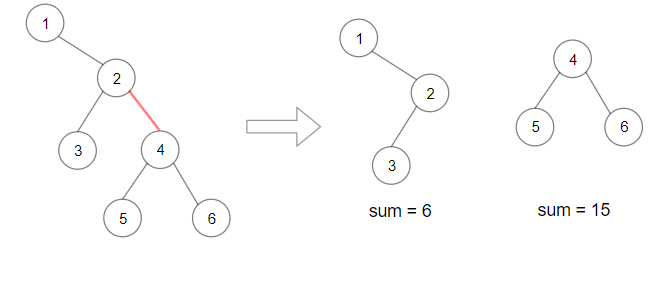
输入:root = [1,null,2,3,4,null,null,5,6]
输出:90
解释:移除红色的边,得到 2 棵子树,和分别是 15 和 6 。它们的乘积为 90 (15*6)
示例 3:
输入:root = [2,3,9,10,7,8,6,5,4,11,1]
输出:1025
示例 4:
输入:root = [1,1]
输出:1
说明:
- 每棵树最多有 50000 个节点,且至少有 2 个节点。
- 每个节点的值在 [1, 10000] 之间。
思路
删除二叉树的一条边,使得产生的两个子树和的乘积最大。
直接的想法是两次遍历,第一次遍历求得所有节点和。第二次遍历则是计算乘积最大值。
可以将子树和保存起来,遍历结束后直接处理和。
注意:求的是最大的乘积然后取模,而非模的最大值。先找出最大的乘积再取模,不能先对乘积取模再比较。
代码
/**
* @date 2026-01-07 8:52
*/
public class MaxProduct1339 {
public long res = 0L;
public int maxProduct(TreeNode root) {
int mod = 1000000007;
int totalSum = dfs(root);
dfs(root, totalSum);
return (int) (res % mod);
}
public int dfs(TreeNode node) {
if (node == null) {
return 0;
}
return node.val + dfs(node.left) + dfs(node.right);
}
public int dfs(TreeNode node, int totalSum) {
if (node == null) {
return 0;
}
int sum = node.val + dfs(node.left, totalSum) + dfs(node.right, totalSum);
res = Math.max(res, (long) sum * (totalSum - sum));
return sum;
}
}
性能