目标
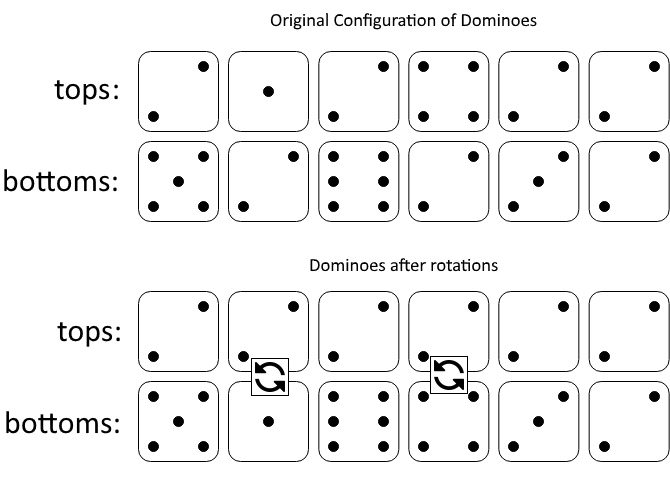
有两种形状的瓷砖:一种是 2 x 1 的多米诺形,另一种是形如 "L" 的托米诺形。两种形状都可以旋转。
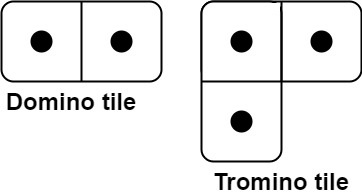
给定整数 n ,返回可以平铺 2 x n 的面板的方法的数量。返回对 10^9 + 7 取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同,当且仅当面板上有四个方向上的相邻单元中的两个,使得恰好有一个平铺有一个瓷砖占据两个正方形。
示例 1:
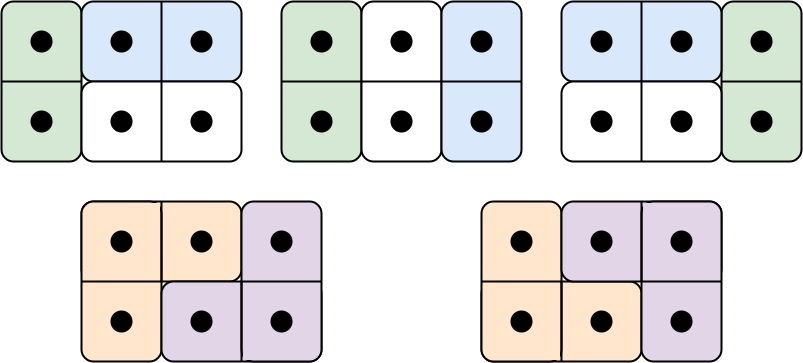
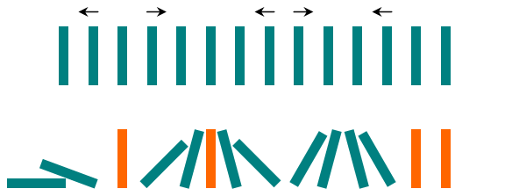
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。示例 2:
输入: n = 1
输出: 1说明:
- 1 <= n <= 1000
思路
有 1 x 2 和 L 型两种形状的瓷砖,求铺满 2 x n 的面版有多少种方法。
题目关于两个平铺是否不同的描述很不清晰,关键在于对 恰好有一个瓷砖 占据两个正方形的理解。
如何判断两种平铺方法是不同的:能找到两个上下相邻的或左右相邻的正方形区域,在其中一种平铺方法中属于同一块瓷砖,在另一种平铺方法中属于不同的瓷砖,则认为这两种平铺方法是不同的。
实际去解决这个问题时可以尝试找规律,通过观察发现:
2 x 1的面版,有1种铺法。2 x 2的面版,有2种铺法。2 x 3的面版,有5种铺法。2 x 4的面版,有11种铺法。2 x 5的面版,有24种铺法。
dp[n] = 2 * dp[n - 1] + dp[n - 3]
如果找不到规律可以参考官网题解的二维动态规划解法。
代码
/**
* @date 2025-05-05 21:37
*/
public class NumTilings790 {
public int numTilings_v1(int n) {
if (n == 1) {
return 1;
}
int mod = 1000000007;
int[] dp = new int[n + 1];
dp[0] = dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = ((2 * dp[i - 1]) % mod + dp[i - 3]) % mod;
}
return dp[n];
}
}
性能