目标
给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积 非零 、边在水平方向和竖直方向上的矩形,并且满足 grid 中所有的 1 都在这些矩形的内部。
返回这些矩形面积之和的 最小 可能值。
注意,这些矩形可以相接。
示例 1:
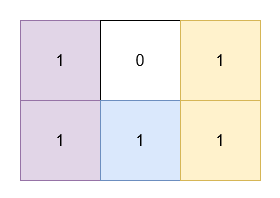
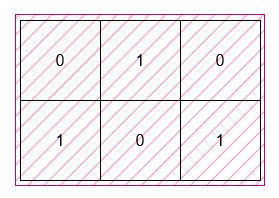
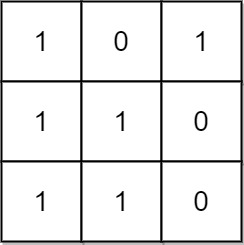
输入: grid = [[1,0,1],[1,1,1]]
输出: 5
解释:
位于 (0, 0) 和 (1, 0) 的 1 被一个面积为 2 的矩形覆盖。
位于 (0, 2) 和 (1, 2) 的 1 被一个面积为 2 的矩形覆盖。
位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。示例 2:
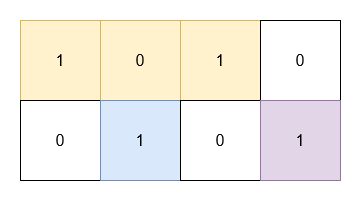
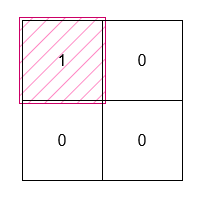
输入: grid = [[1,0,1,0],[0,1,0,1]]
输出: 5
解释:
位于 (0, 0) 和 (0, 2) 的 1 被一个面积为 3 的矩形覆盖。
位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。
位于 (1, 3) 的 1 被一个面积为 1 的矩形覆盖。说明:
- 1 <= grid.length, grid[i].length <= 30
grid[i][j]是 0 或 1。- 输入保证 grid 中至少有三个 1 。
思路
代码