目标
小红和小明在玩一个字符串元音游戏。
给你一个字符串 s,小红和小明将轮流参与游戏,小红 先 开始:
- 在小红的回合,她必须移除 s 中包含 奇数 个元音的任意 非空 子字符串。
- 在小明的回合,他必须移除 s 中包含 偶数 个元音的任意 非空 子字符串。
第一个无法在其回合内进行移除操作的玩家输掉游戏。假设小红和小明都采取 最优策略 。
如果小红赢得游戏,返回 true,否则返回 false。
英文元音字母包括:a, e, i, o, 和 u。
示例 1:
输入: s = "leetcoder"
输出: true
解释:
小红可以执行如下移除操作来赢得游戏:
小红先手,她可以移除加下划线的子字符串 s = "leetcoder",其中包含 3 个元音。结果字符串为 s = "der"。
小明接着,他可以移除加下划线的子字符串 s = "der",其中包含 0 个元音。结果字符串为 s = "er"。
小红再次操作,她可以移除整个字符串 s = "er",其中包含 1 个元音。
又轮到小明,由于字符串为空,无法执行移除操作,因此小红赢得游戏。示例 2:
输入: s = "bbcd"
输出: false
解释:
小红在她的第一回合无法执行移除操作,因此小红输掉了游戏。说明:
- 1 <= s.length <= 10^5
- s 仅由小写英文字母组成。
思路
小红与小明在玩字符串元音游戏,小红的回合必须移除包含 奇数 个元音的任意非空子串,小明的回合必须移除包含 偶数 个元音的任意非空子串。如果无法完成操作则输掉游戏,假设小红和小明都采取最优策略,判断小红能否赢得游戏。
如果字符串中包含奇数个元音字符,小红必定获胜。否则,小红应该移除最大的奇数个元音字符,这时剩余一个元音字符,小明只能删除不含元音字符的子串,这时小红将剩余的子串全部删掉,就赢得了游戏。
因此只要字符包含元音字符,小红必定获胜。
代码
/**
* @date 2025-09-12 8:43
*/
public class DoesAliceWin3227 {
public boolean doesAliceWin(String s) {
char[] chars = s.toCharArray();
for (char c : chars) {
if (c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u') {
return true;
}
}
return false;
}
}
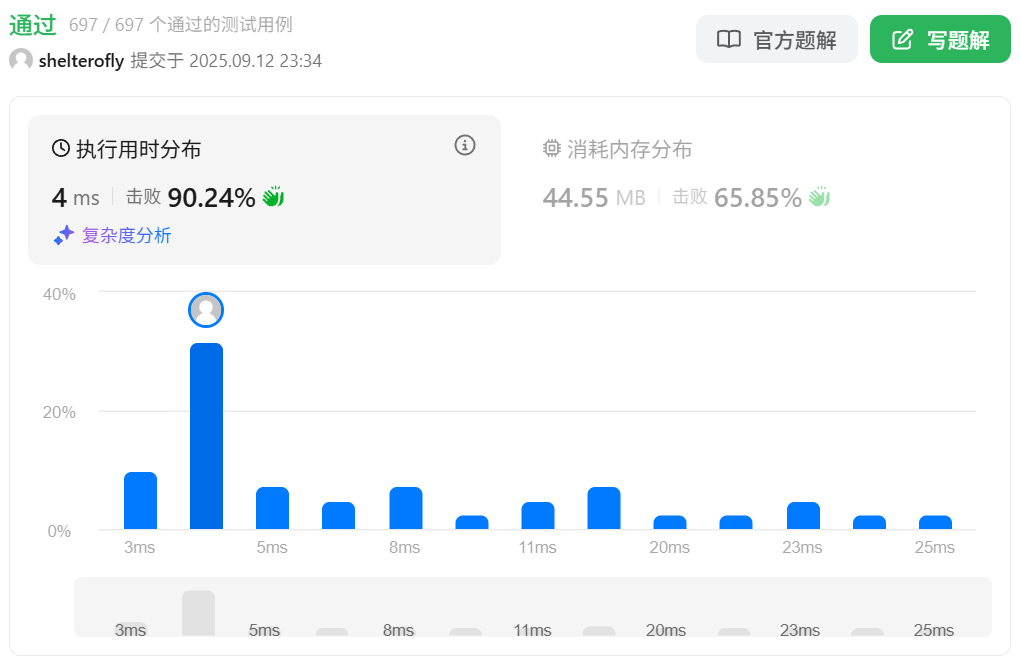
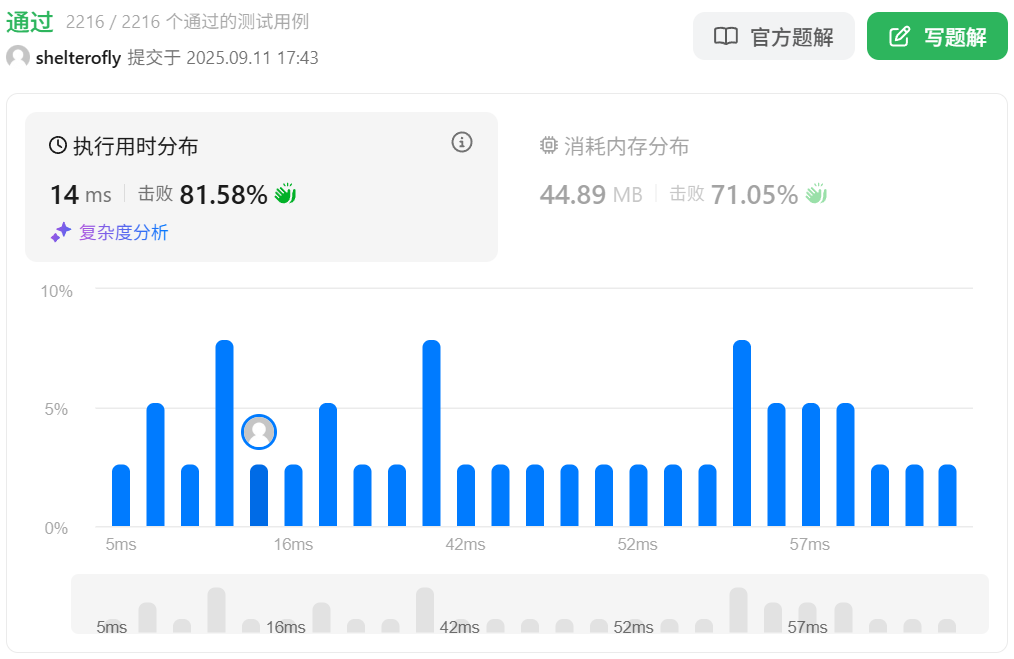
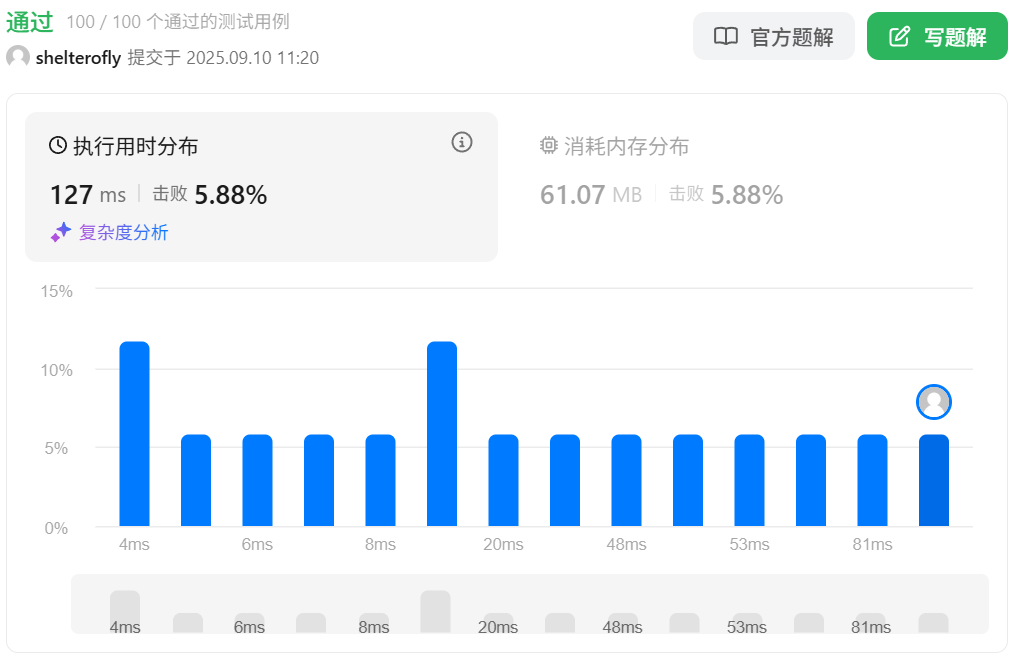
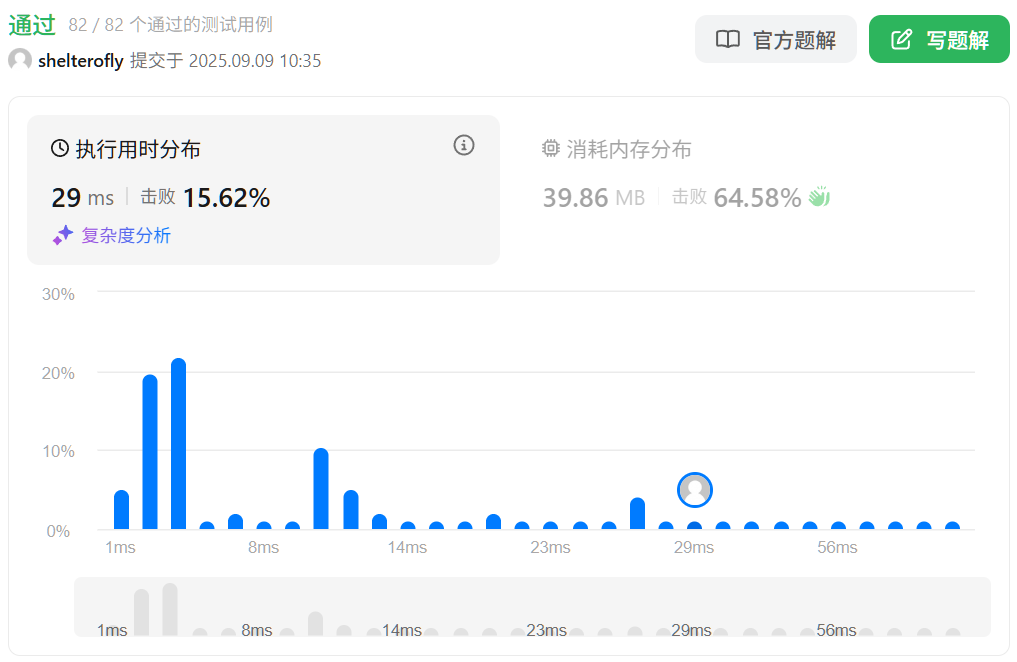
性能