目标
给定由 n 个字符串组成的数组 strs,其中每个字符串长度相等。
选取一个删除索引序列,对于 strs 中的每个字符串,删除对应每个索引处的字符。
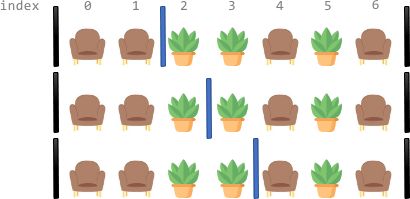
比如,有 strs = ["abcdef", "uvwxyz"],删除索引序列 {0, 2, 3},删除后 strs 为["bef", "vyz"]。
假设,我们选择了一组删除索引 answer,那么在执行删除操作之后,最终得到的数组的元素是按 字典序(strs[0] <= strs[1] <= strs[2] ... <= strs[n - 1])排列的,然后请你返回 answer.length 的最小可能值。
示例 1:
输入:strs = ["ca","bb","ac"]
输出:1
解释:
删除第一列后,strs = ["a", "b", "c"]。
现在 strs 中元素是按字典排列的 (即,strs[0] <= strs[1] <= strs[2])。
我们至少需要进行 1 次删除,因为最初 strs 不是按字典序排列的,所以答案是 1。示例 2:
输入:strs = ["xc","yb","za"]
输出:0
解释:
strs 的列已经是按字典序排列了,所以我们不需要删除任何东西。
注意 strs 的行不需要按字典序排列。
也就是说,strs[0][0] <= strs[0][1] <= ... 不一定成立。示例 3:
输入:strs = ["zyx","wvu","tsr"]
输出:3
解释:
我们必须删掉每一列。说明:
- n == strs.length
- 1 <= n <= 100
- 1 <= strs[i].length <= 100
- strs[i] 由小写英文字母组成
思路
有一个元素长度相同的字符串数组 strs,通过删除列使得字符串元素按字典序非严格递增,返回删除的最少列数。
首先如果按列不是非严格递增的,那么一定要删除该列。然后,如果是非严格递增的,需要继续考查相同行后续列的字典序。
维护同一列中相同字母的行标列表 sameList,初始时包括所有行,如果需要删除就直接进入下一列循环,否则遍历 sameList 判断是否是升序(相同的字母组内比较),同时记录当前列相同的行标,如果 sameList 列表为空则退出。
代码
/**
* @date 2025-12-21 19:24
*/
public class MinDeletionSize955 {
public int minDeletionSize(String[] strs) {
int n = strs.length;
int m = strs[0].length();
List<Integer> indexList = new ArrayList<>(n);
for (int i = 0; i < n - 1; i++) {
indexList.add(i);
}
int res = 0;
here:
for (int i = 0; i < m; i++) {
if (indexList.size() == 0) {
break;
}
List<Integer> tmp = new ArrayList<>();
for (Integer k : indexList) {
char cur = strs[k].charAt(i);
char next = strs[k + 1].charAt(i);
if (cur > next) {
res++;
continue here;
} else if (cur == next) {
tmp.add(k);
}
}
indexList = tmp;
}
return res;
}
}
性能