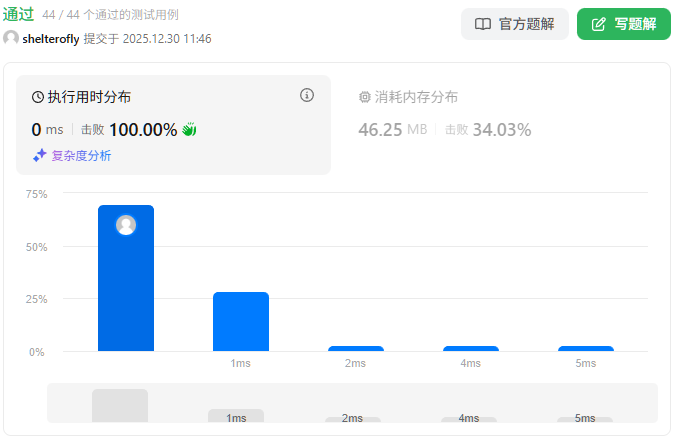
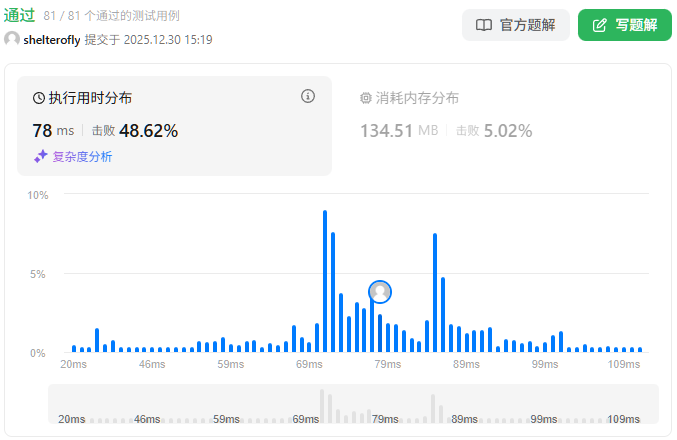
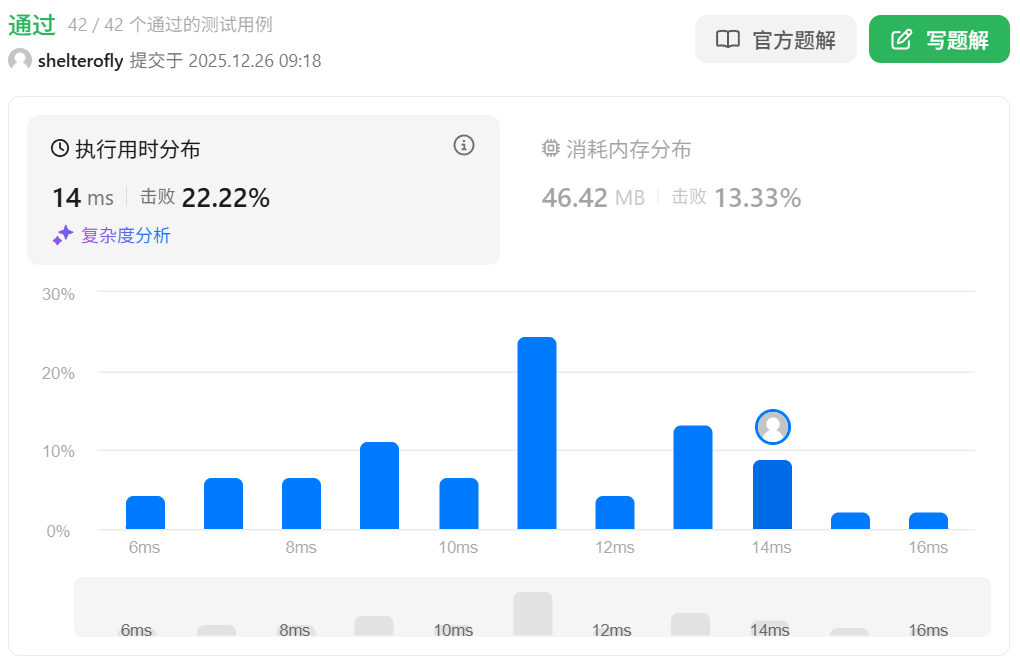
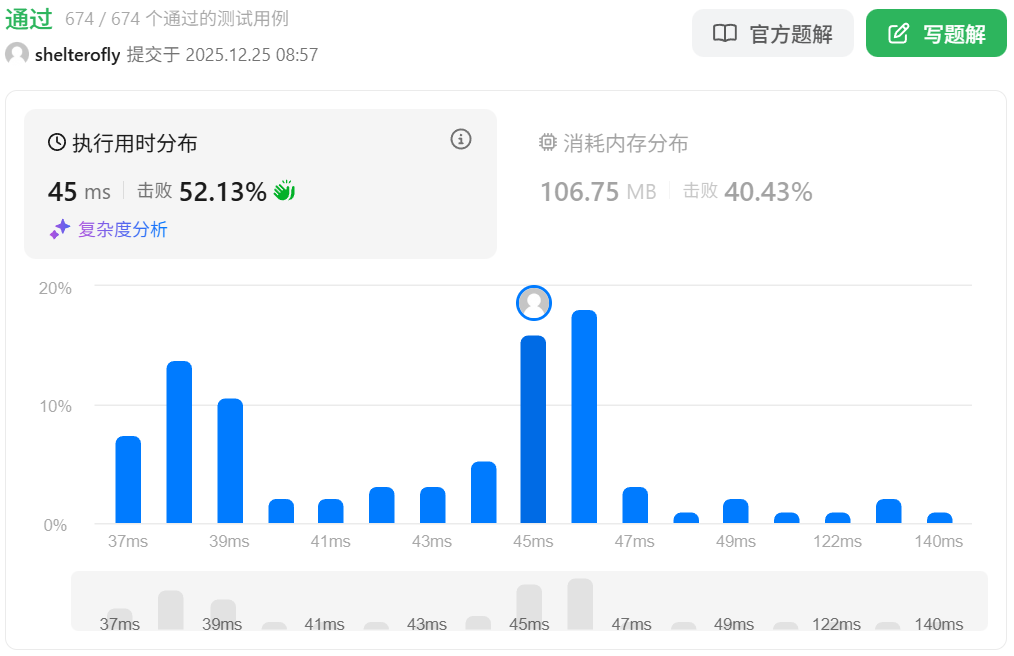
目标
给你一个下标从 1 开始的二进制矩阵,其中 0 表示陆地,1 表示水域。同时给你 row 和 col 分别表示矩阵中行和列的数目。
一开始在第 0 天,整个 矩阵都是 陆地 。但每一天都会有一块新陆地被 水 淹没变成水域。给你一个下标从 1 开始的二维数组 cells ,其中 cells[i] = [ri, ci] 表示在第 i 天,第 ri 行 ci 列(下标都是从 1 开始)的陆地会变成 水域 (也就是 0 变成 1 )。
你想知道从矩阵最 上面 一行走到最 下面 一行,且只经过陆地格子的 最后一天 是哪一天。你可以从最上面一行的 任意 格子出发,到达最下面一行的 任意 格子。你只能沿着 四个 基本方向移动(也就是上下左右)。
请返回只经过陆地格子能从最 上面 一行走到最 下面 一行的 最后一天 。
示例 1:

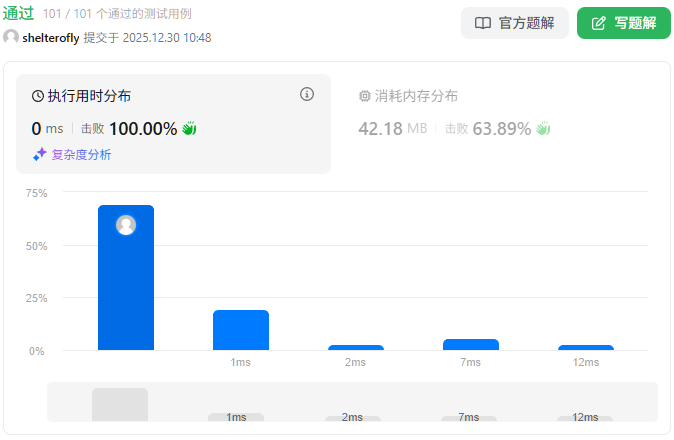
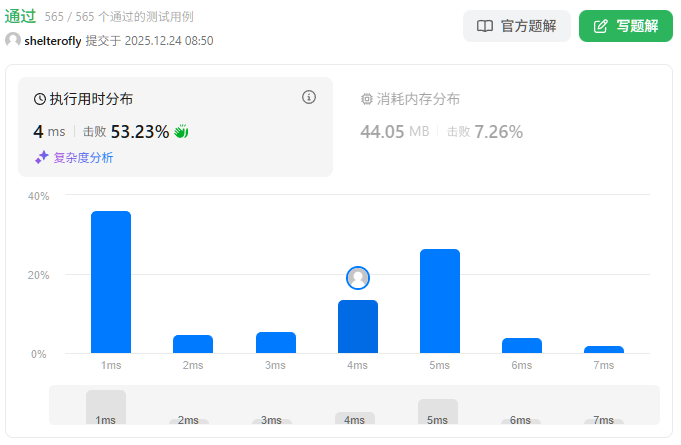
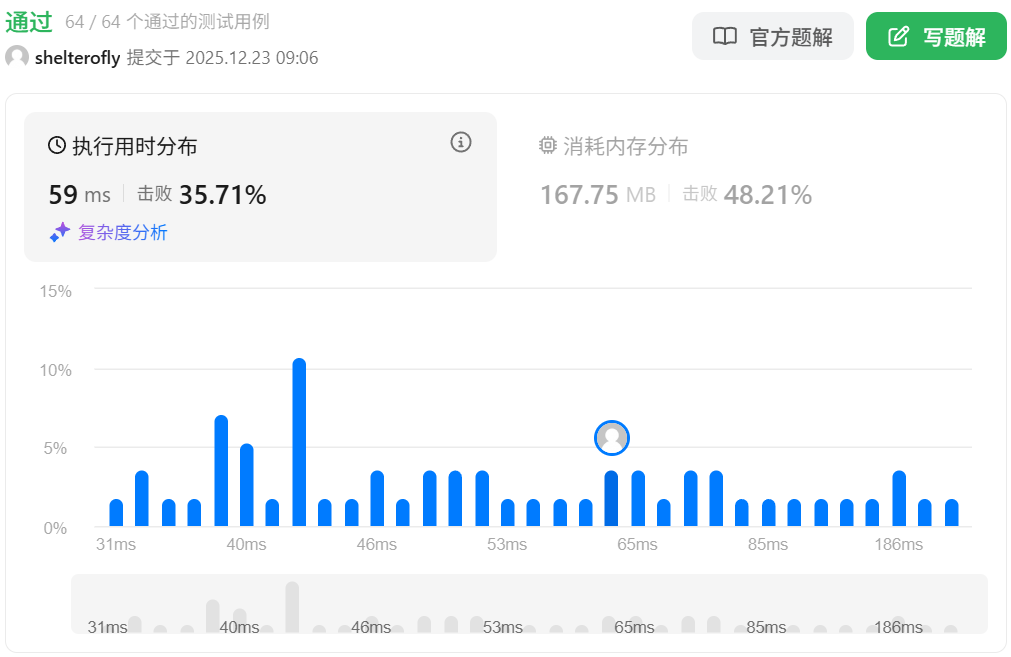
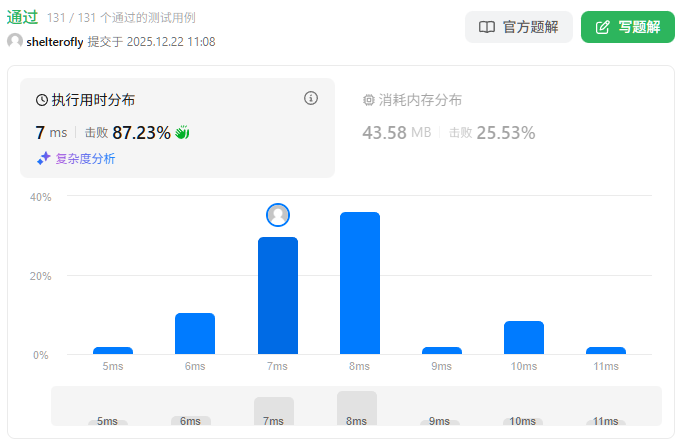
输入:row = 2, col = 2, cells = [[1,1],[2,1],[1,2],[2,2]]
输出:2
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 2 天。示例 2:
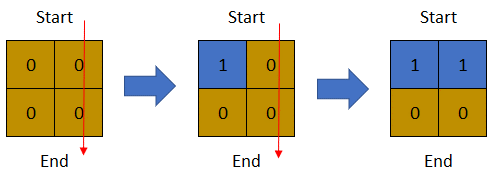
输入:row = 2, col = 2, cells = [[1,1],[1,2],[2,1],[2,2]]
输出:1
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 1 天。示例 3:

输入:row = 3, col = 3, cells = [[1,2],[2,1],[3,3],[2,2],[1,1],[1,3],[2,3],[3,2],[3,1]]
输出:3
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 3 天。说明:
- 2 <= row, col <= 2 * 10^4
- 4 <= row col <= 2 10^4
- cells.length == row * col
- 1 <= ri <= row
- 1 <= ci <= col
- cells 中的所有格子坐标都是 唯一 的。
思路
有一个二进制矩阵,0 代表陆地,1 代表水域。第 0 天,整个矩阵都是陆地,之后的每一天都会有一块陆地变为水域,cells[i] = [rowi, coli] 表示第 i + 1 天,矩阵的 rowi 行,coli 列会变为水域,注意行列的下标从 1 开始。返回能从第一行走到最后一行的最后一天是哪天。
BFS 可用于判断路径是否存在,二分答案判断即可。
代码
/**
* @date 2025-12-31 9:56
*/
public class LatestDayToCross1970 {
public int latestDayToCross(int row, int col, int[][] cells) {
int l = 0, r = cells.length - 1;
int m = l + (r - l) / 2;
while (l <= r) {
if (check(row, col, m, cells)) {
l = m + 1;
} else {
r = m - 1;
}
m = l + (r - l) / 2;
}
return r;
}
public int[][] directions = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public boolean check(int row, int col, int m, int[][] cells) {
int[][] grid = new int[row + 1][col + 1];
for (int i = 0; i < m; i++) {
grid[cells[i][0]][cells[i][1]] = 1;
}
Deque<int[]> q = new ArrayDeque<>();
for (int i = 1; i <= col; i++) {
if (grid[1][i] == 0) {
grid[1][i] = 1;
q.offer(new int[]{1, i});
}
}
while (!q.isEmpty()) {
int size = q.size();
for (int i = 0; i < size; i++) {
int[] cur = q.poll();
for (int[] direction : directions) {
int x = cur[0] + direction[0];
int y = cur[1] + direction[1];
if (x >= 1 && x <= row && y >= 1 && y <= col && grid[x][y] == 0) {
if (x == row) {
return true;
}
grid[x][y] = 1;
q.offer(new int[]{x, y});
}
}
}
}
return false;
}
}
性能