分类： leetcode

目标

给你一个字符串 s 和两个整数 x 和 y 。你可以执行下面两种操作任意次。

• 删除子字符串 "ab" 并得到 x 分。
  • 比方说，从 "cabxbae" 删除 ab ，得到 "cxbae" 。
• 删除子字符串"ba" 并得到 y 分。
  • 比方说，从 "cabxbae" 删除 ba ，得到 "cabxe" 。

请返回对 s 字符串执行上面操作若干次能得到的最大得分。

示例 1：

输入：s = "cdbcbbaaabab", x = 4, y = 5
输出：19
解释：
- 删除 "cdbcbbaaabab" 中加粗的 "ba" ，得到 s = "cdbcbbaaab" ，加 5 分。
- 删除 "cdbcbbaaab" 中加粗的 "ab" ，得到 s = "cdbcbbaa" ，加 4 分。
- 删除 "cdbcbbaa" 中加粗的 "ba" ，得到 s = "cdbcba" ，加 5 分。
- 删除 "cdbcba" 中加粗的 "ba" ，得到 s = "cdbc" ，加 5 分。
总得分为 5 + 4 + 5 + 5 = 19 。

示例 2：

输入：s = "aabbaaxybbaabb", x = 5, y = 4
输出：20

说明：

• 1 <= s.length <= 10^5
• 1 <= x, y <= 10^4
• s 只包含小写英文字母。

思路

贪心策略，优先处理分值高的字符串。

代码

/**
 * @date 2025-07-23 9:01
 */
public class MaximumGain1717 {

    public int maximumGain(String s, int x, int y) {
        char prev, cur;
        int max, min;
        if (x > y) {
            prev = 'a';
            cur = 'b';
            max = x;
            min = y;
        } else {
            prev = 'b';
            cur = 'a';
            max = y;
            min = x;
        }
        Deque<Character> q = new ArrayDeque<>();
        q.push('^');
        int n = s.length();
        int res = 0;
        for (int i = 0; i < n; i++) {
            char c = s.charAt(i);
            if (q.peek() == prev && c == cur) {
                q.pop();
                res += max;
            } else {
                q.push(c);
            }
        }
        q.removeLast();
        Deque<Character> p = new ArrayDeque<>();
        p.push('^');
        while (!q.isEmpty()) {
            if (q.peekLast() == prev && p.peek() == cur) {
                q.removeLast();
                p.pop();
                res += min;
            } else {
                p.push(q.removeLast());
            }
        }
        return res;
    }

}

性能

目标

给你一个正整数数组 nums ，请你从中删除一个含有 若干不同元素 的子数组。删除子数组的 得分 就是子数组各元素之 和 。

返回 只删除一个 子数组可获得的 最大得分 。

如果数组 b 是数组 a 的一个连续子序列，即如果它等于 a[l],a[l+1],...,a[r] ，那么它就是 a 的一个子数组。

示例 1：

输入：nums = [4,2,4,5,6]
输出：17
解释：最优子数组是 [2,4,5,6]

示例 2：

输入：nums = [5,2,1,2,5,2,1,2,5]
输出：8
解释：最优子数组是 [5,2,1] 或 [1,2,5]

说明：

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^4

思路

有一个正整数数组 nums，求一个不含重复元素的子数组，使得子数组的元素和最大。

滑动窗口，要求窗口内部不含重复元素，求窗口内元素和的最大值。

代码

/**
 * @date 2025-07-22 8:50
 */
public class MaximumUniqueSubarray1695 {

    public int maximumUniqueSubarray(int[] nums) {
        int n = nums.length;
        Set<Integer> set = new HashSet<>();
        int l = 0;
        int sum = 0;
        int res = 0;
        for (int r = 0; r < n; r++) {
            sum += nums[r];
            while (l < r && set.contains(nums[r])) {
                sum -= nums[l];
                set.remove(nums[l++]);
            }
            set.add(nums[r]);
            res = Math.max(res, sum);
        }
        return res;
    }

}

性能

目标

你是一位系统管理员，手里有一份文件夹列表 folder，你的任务是要删除该列表中的所有 子文件夹，并以 任意顺序 返回剩下的文件夹。

如果文件夹 folder[i] 位于另一个文件夹 folder[j] 下，那么 folder[i] 就是 folder[j] 的 子文件夹 。folder[j] 的子文件夹必须以 folder[j] 开头，后跟一个 "/"。例如，"/a/b" 是 "/a" 的一个子文件夹，但 "/b" 不是 "/a/b/c" 的一个子文件夹。

文件夹的「路径」是由一个或多个按以下格式串联形成的字符串：'/' 后跟一个或者多个小写英文字母。

• 例如，"/leetcode" 和 "/leetcode/problems" 都是有效的路径，而空字符串和 "/" 不是。

示例 1：

输入：folder = ["/a","/a/b","/c/d","/c/d/e","/c/f"]
输出：["/a","/c/d","/c/f"]
解释："/a/b" 是 "/a" 的子文件夹，而 "/c/d/e" 是 "/c/d" 的子文件夹。

示例 2：

输入：folder = ["/a","/a/b/c","/a/b/d"]
输出：["/a"]
解释：文件夹 "/a/b/c" 和 "/a/b/d" 都会被删除，因为它们都是 "/a" 的子文件夹。

示例 3：

输入: folder = ["/a/b/c","/a/b/ca","/a/b/d"]
输出: ["/a/b/c","/a/b/ca","/a/b/d"]

说明：

• 1 <= folder.length <= 4 * 10^4
• 2 <= folder[i].length <= 100
• folder[i] 只包含小写字母和 '/'
• folder[i] 总是以字符 '/' 起始
• folder 每个元素都是 唯一 的

思路

有一个文件夹列表，删除其中所有的子文件夹。

将文件夹列表排序，父目录总是会先出现，记为 prev，使用 startsWith 判断当前目录是否是子目录，如果不是更新 prev，并加入结果集合，否则直接跳过。需要注意 prev 需要以 / 结尾，否则会错误地匹配，比如 /a/b/c 并不是 /a/b/ca 的父目录。

也可以使用字典树来解决该问题，构造字典树，将最后一个节点标记为文件夹列表的下标，dfs 字典树，如果遇到标记非空则直接返回，不再查找子文件夹。

代码

/**
 * @date 2025-07-19 10:57
 */
public class RemoveSubfolders1233 {

    public List<String> removeSubfolders(String[] folder) {
        Arrays.sort(folder);
        String prev = ".";
        List<String> res = new ArrayList<>();
        for (String path : folder) {
            if (path.startsWith(prev)) {
                continue;
            }
            res.add(path);
            prev = path + "/";
        }
        return res;
    }

}

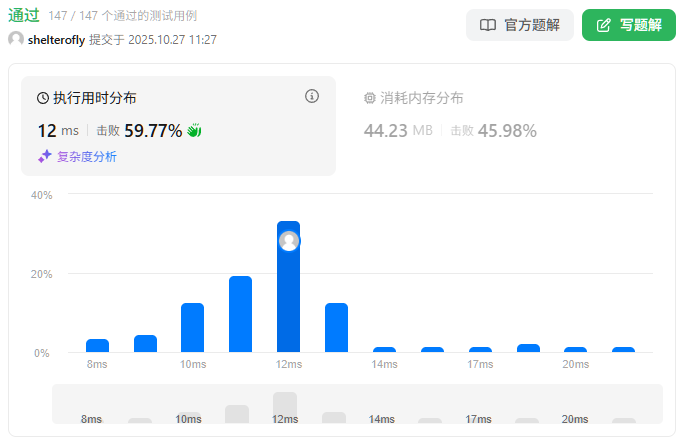
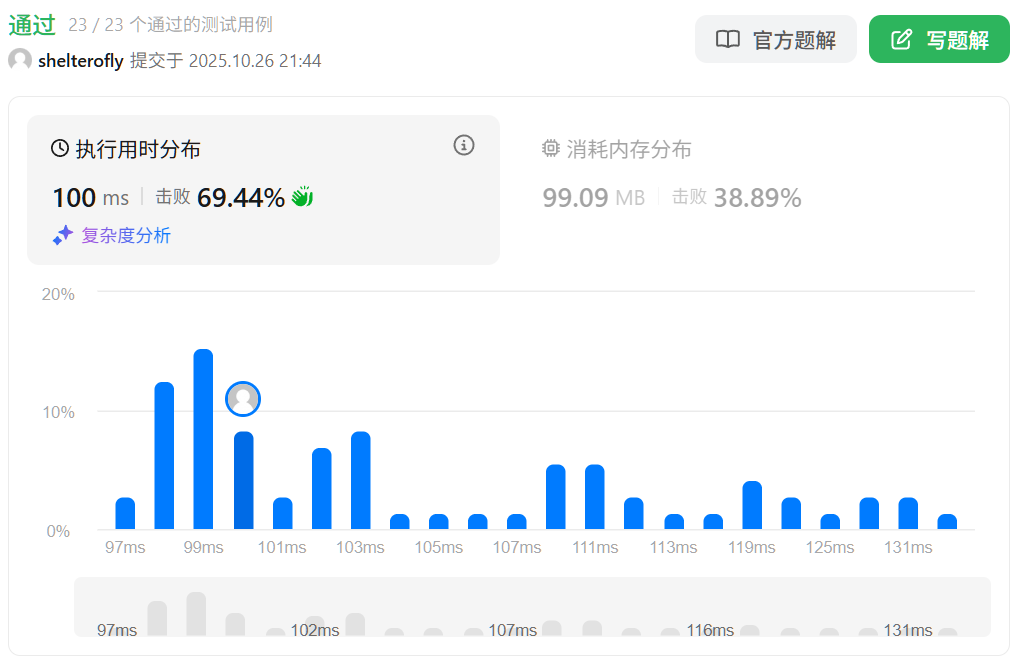
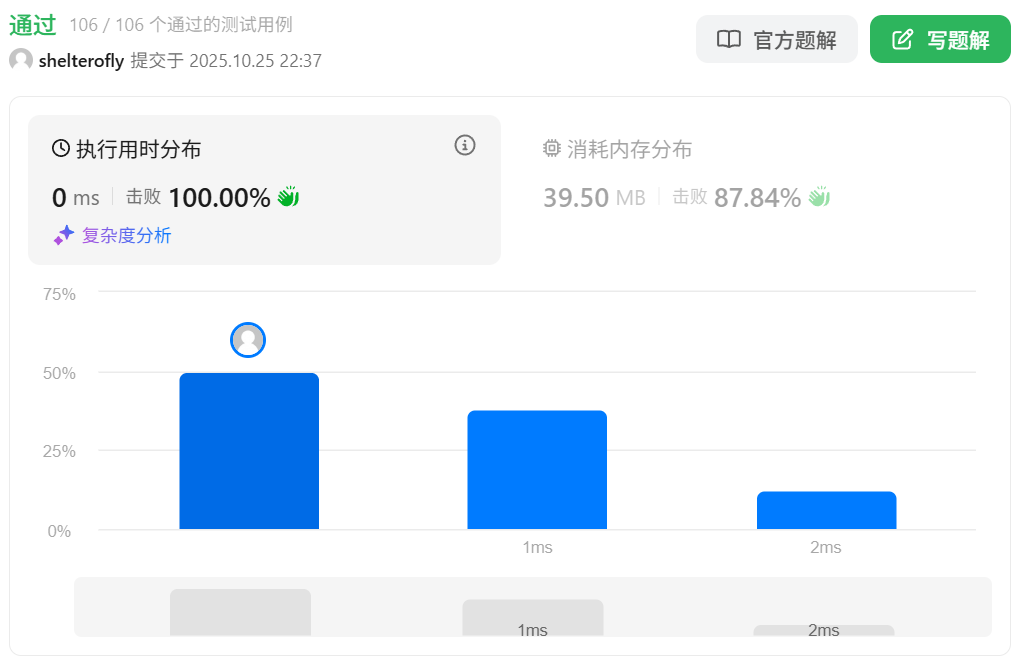
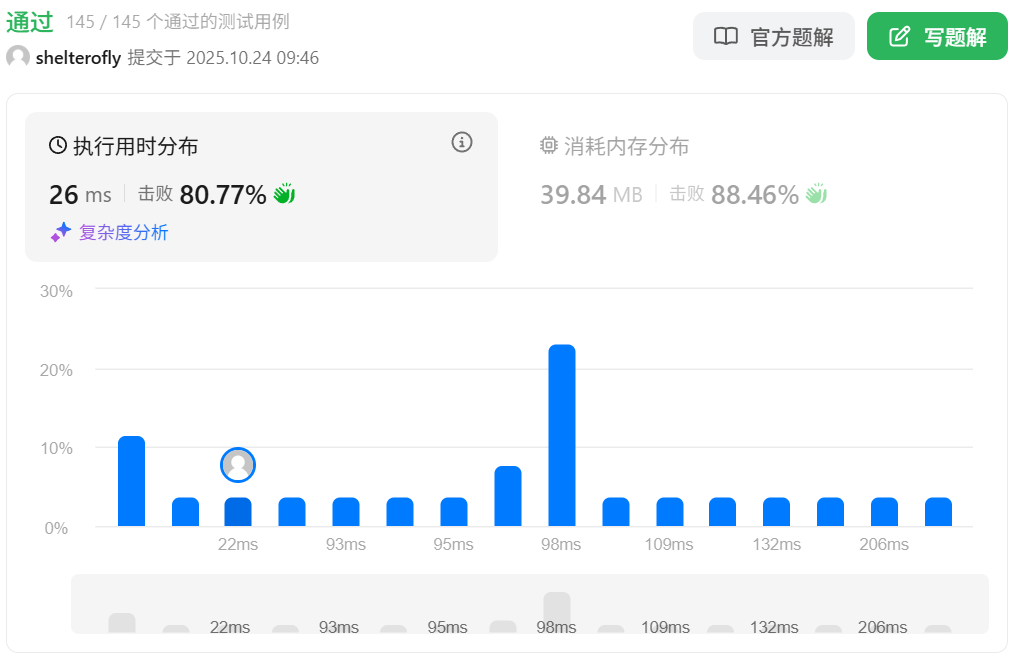
性能