目标
给你一个正整数 n,表示一个 n x n 的城市,同时给定一个二维数组 buildings,其中 buildings[i] = [x, y] 表示位于坐标 [x, y] 的一个 唯一 建筑。
如果一个建筑在四个方向(左、右、上、下)中每个方向上都至少存在一个建筑,则称该建筑 被覆盖 。
返回 被覆盖 的建筑数量。
示例 1:
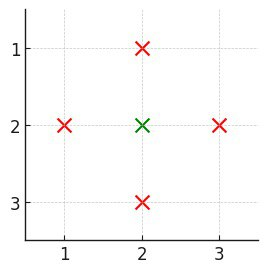
输入: n = 3, buildings = [[1,2],[2,2],[3,2],[2,1],[2,3]]
输出: 1
解释:
只有建筑 [2,2] 被覆盖,因为它在每个方向上都至少存在一个建筑:
上方 ([1,2])
下方 ([3,2])
左方 ([2,1])
右方 ([2,3])
因此,被覆盖的建筑数量是 1。示例 2:
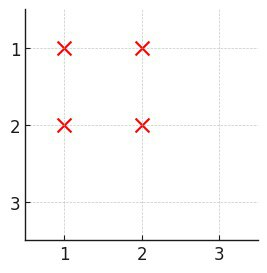
输入: n = 3, buildings = [[1,1],[1,2],[2,1],[2,2]]
输出: 0
解释:
没有任何一个建筑在每个方向上都有至少一个建筑。示例 3:
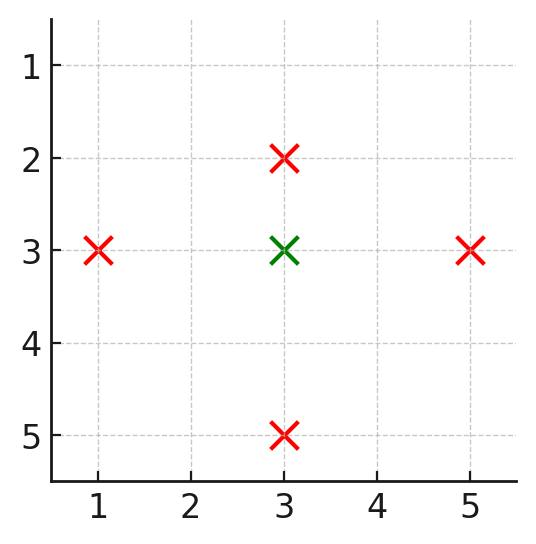
输入: n = 5, buildings = [[1,3],[3,2],[3,3],[3,5],[5,3]]
输出: 1
解释:
只有建筑 [3,3] 被覆盖,因为它在每个方向上至少存在一个建筑:
上方 ([1,3])
下方 ([5,3])
左方 ([3,2])
右方 ([3,5])
因此,被覆盖的建筑数量是 1。说明:
- 2 <= n <= 10^5
- 1 <= buildings.length <= 10^5
- buildings[i] = [x, y]
- 1 <= x, y <= n
- buildings 中所有坐标均 唯一 。
思路
二维数组 buildings 表示建筑的坐标,如果建筑的上下左右均存在其它建筑,则称该建筑被包围。统计被包围建筑的个数。
只需记录每一行每一列的最大值与最小值,判断当前建筑是否在其中。
代码
/**
* @date 2025-12-11 14:03
*/
public class CountCoveredBuildings3531 {
public int countCoveredBuildings_v1(int n, int[][] buildings) {
int[] minX = new int[n + 1];
int[] maxX = new int[n + 1];
int[] minY = new int[n + 1];
int[] maxY = new int[n + 1];
Arrays.fill(minX, n + 1);
Arrays.fill(minY, n + 1);
for (int[] building : buildings) {
int x = building[0];
int y = building[1];
minX[y] = Math.min(minX[y], x);
maxX[y] = Math.max(maxX[y], x);
minY[x] = Math.min(minY[x], y);
maxY[x] = Math.max(maxY[x], y);
}
int res = 0;
for (int[] building : buildings) {
int x = building[0];
int y = building[1];
if (x > minX[y] && x < maxX[y] && y > minY[x] && y < maxY[x]) {
res++;
}
}
return res;
}
}
性能