目标
给你两个字符串 coordinate1 和 coordinate2,代表 8 x 8 国际象棋棋盘上的两个方格的坐标。
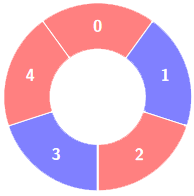
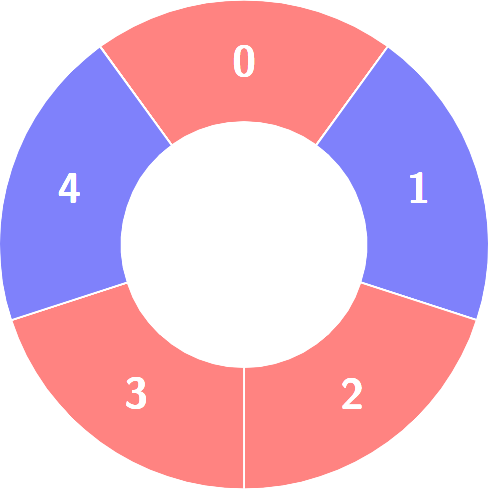
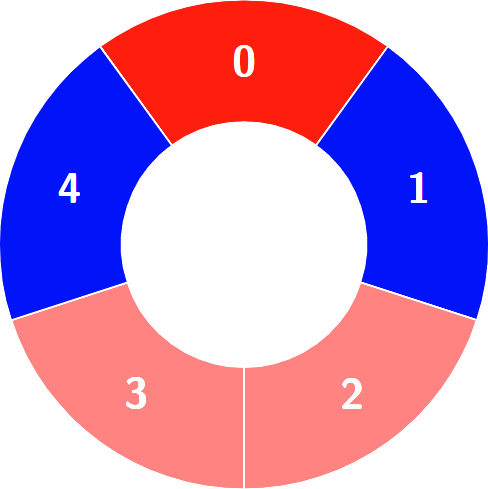
以下是棋盘的参考图。

如果这两个方格颜色相同,返回 true,否则返回 false。
坐标总是表示有效的棋盘方格。坐标的格式总是先字母(表示列),再数字(表示行)。
示例 1:
输入: coordinate1 = "a1", coordinate2 = "c3"
输出: true
解释:
两个方格均为黑色。示例 2:
输入: coordinate1 = "a1", coordinate2 = "h3"
输出: false
解释:
方格 "a1" 是黑色,而 "h3" 是白色。说明:
- coordinate1.length == coordinate2.length == 2
- 'a' <= coordinate1[0], coordinate2[0] <= 'h'
- '1' <= coordinate1[1], coordinate2[1] <= '8'
思路
有一个棋盘行列从 1、a 开始编号,奇数列(a c e g)奇数行(1 3 5 7)是黑色,奇数列偶数行是白色;偶数列奇数行是白色,偶数列偶数行是黑色。判断给定的两个格子颜色是否相同。
如果两个坐标的列编号奇偶性相同,要想使颜色相同,那么行编号的奇偶性也应相同。换句话说就是判断给定的横纵坐标编号的奇偶性是否同时相等或不等。
代码
/**
* @date 2024-12-03 8:58
*/
public class CheckTwoChessboards3274 {
public boolean checkTwoChessboards_v1(String coordinate1, String coordinate2) {
return (coordinate1.charAt(0) + coordinate1.charAt(1)) % 2 == (coordinate2.charAt(0) + coordinate2.charAt(1)) % 2;
}
public boolean checkTwoChessboards(String coordinate1, String coordinate2) {
int x1 = coordinate1.charAt(0) - 'a';
int y1 = coordinate1.charAt(1) - '1';
int x2 = coordinate2.charAt(0) - 'a';
int y2 = coordinate2.charAt(1) - '1';
if (x1 % 2 == x2 % 2) {
return y1 % 2 == y2 % 2;
} else {
return y1 % 2 != y2 % 2;
}
}
}
性能