目标
给你一个整数数组 nums ,一个整数 k 和一个整数 multiplier 。
你需要对 nums 执行 k 次操作,每次操作中:
- 找到 nums 中的 最小 值 x ,如果存在多个最小值,选择最 前面 的一个。
- 将 x 替换为 x * multiplier 。
请你返回执行完 k 次乘运算之后,最终的 nums 数组。
示例 1:
输入:nums = [2,1,3,5,6], k = 5, multiplier = 2
输出:[8,4,6,5,6]
解释:
操作 结果
1 次操作后 [2, 2, 3, 5, 6]
2 次操作后 [4, 2, 3, 5, 6]
3 次操作后 [4, 4, 3, 5, 6]
4 次操作后 [4, 4, 6, 5, 6]
5 次操作后 [8, 4, 6, 5, 6]示例 2:
输入:nums = [1,2], k = 3, multiplier = 4
输出:[16,8]
解释:
操作 结果
1 次操作后 [4, 2]
2 次操作后 [4, 8]
3 次操作后 [16, 8]说明:
- 1 <= nums.length <= 100
- 1 <= nums[i] <= 100
- 1 <= k <= 10
- 1 <= multiplier <= 5
思路
有一个数组 nums,我们需要执行 k 次操作,每次操作选择数组中最小元素 min,并将它的值替换为 min * multiplier,返回最终的数组。
使用最小堆,堆中元素为 [value, index],获取堆顶元素,将其值乘以 multiplier 再放回堆中,操作完 k 次之后,遍历堆中元素,根据 index 重写 nums 即可。需要注意处理值相等的情况,堆排序不稳定。
代码
/**
* @date 2024-12-13 2:13
*/
public class GetFinalState3264 {
public int[] getFinalState(int[] nums, int k, int multiplier) {
int n = nums.length;
// 注意这里需要处理相等的情况,堆排序是不稳定的
PriorityQueue<Integer> q = new PriorityQueue<>((a, b) -> {
int compare = nums[a] - nums[b];
if (compare != 0){
return compare;
}
return a - b;
});
for (int i = 0; i < n; i++) {
q.offer(i);
}
for (int i = 0; i < k; i++) {
int index = q.poll();
nums[index] *= multiplier;
q.offer(index);
}
return nums;
}
}
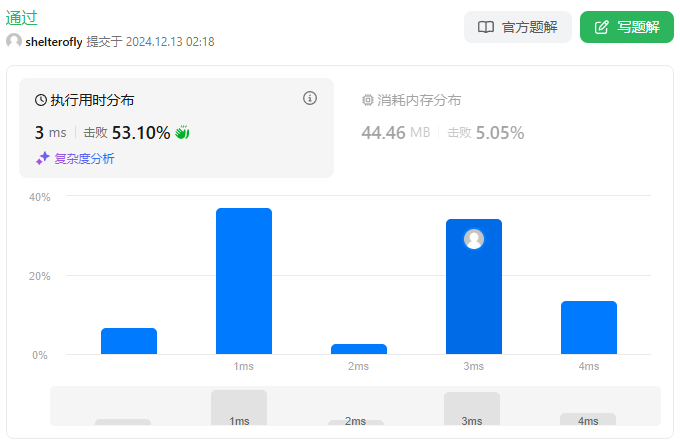
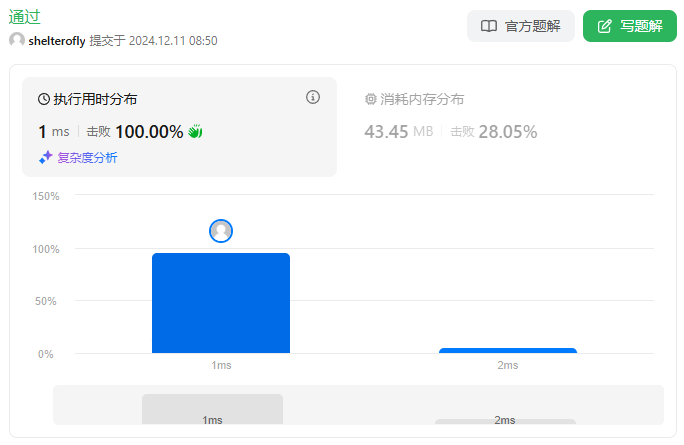
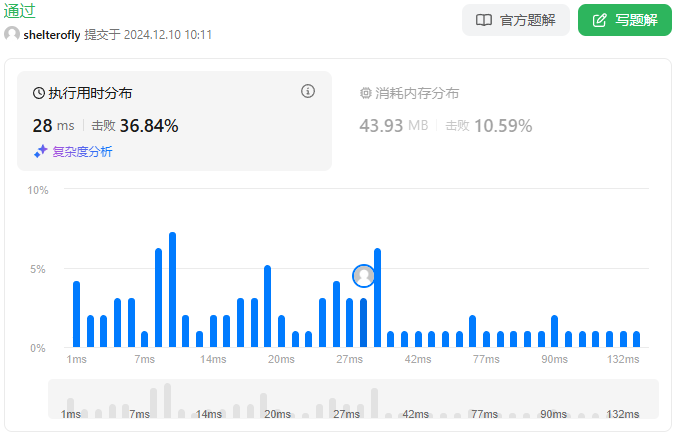
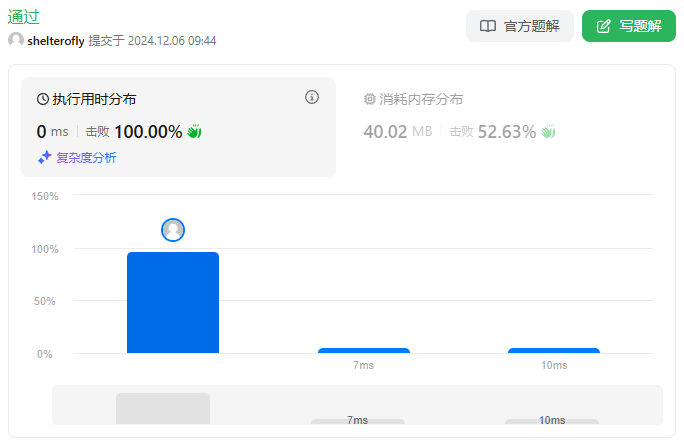
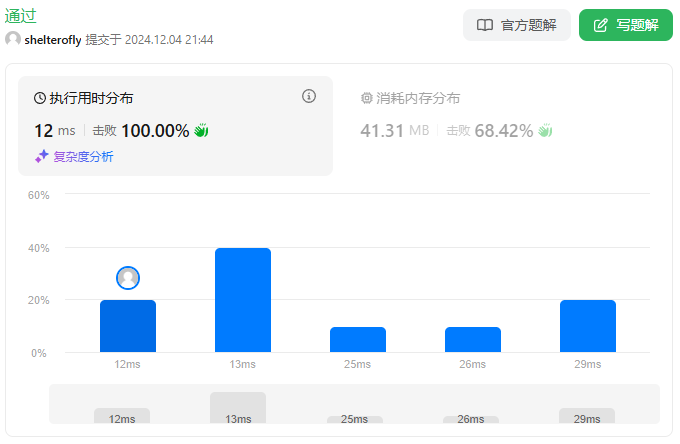
性能