目标
在一个无限的 x 坐标轴上,有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ,其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ,每个 positioni 互不相同 。
另给你两个整数 startPos 和 k 。最初,你位于 startPos 。从任何位置,你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ,就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置,都会摘掉全部的水果,水果也将从该位置消失(不会再生)。
返回你可以摘到水果的 最大总数 。
示例 1:
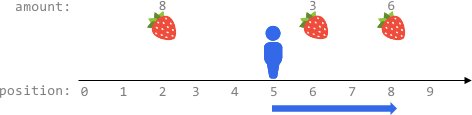
输入:fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出:9
解释:
最佳路线为:
- 向右移动到位置 6 ,摘到 3 个水果
- 向右移动到位置 8 ,摘到 6 个水果
移动 3 步,共摘到 3 + 6 = 9 个水果示例 2:
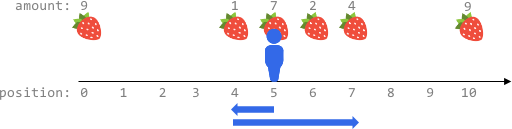
输入:fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出:14
解释:
可以移动最多 k = 4 步,所以无法到达位置 0 和位置 10 。
最佳路线为:
- 在初始位置 5 ,摘到 7 个水果
- 向左移动到位置 4 ,摘到 1 个水果
- 向右移动到位置 6 ,摘到 2 个水果
- 向右移动到位置 7 ,摘到 4 个水果
移动 1 + 3 = 4 步,共摘到 7 + 1 + 2 + 4 = 14 个水果示例 3:
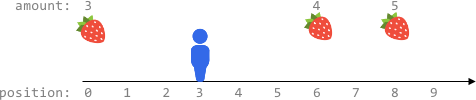
输入:fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出:0
解释:
最多可以移动 k = 2 步,无法到达任一有水果的地方说明:
- 1 <= fruits.length <= 10^5
- fruits[i].length == 2
- 0 <= startPos, positioni <= 2 * 10^5
- 对于任意 i > 0 ,positioni-1 < positioni 均成立(下标从 0 开始计数)
- 1 <= amounti <= 10^4
- 0 <= k <= 2 * 10^5
思路
代码