目标
给你一个由 X-Y 平面上的点组成的数组 points ,其中 points[i] = [xi, yi] 。从其中取任意三个不同的点组成三角形,返回能组成的最大三角形的面积。与真实值误差在 10^-5 内的答案将会视为正确答案。
示例 1:
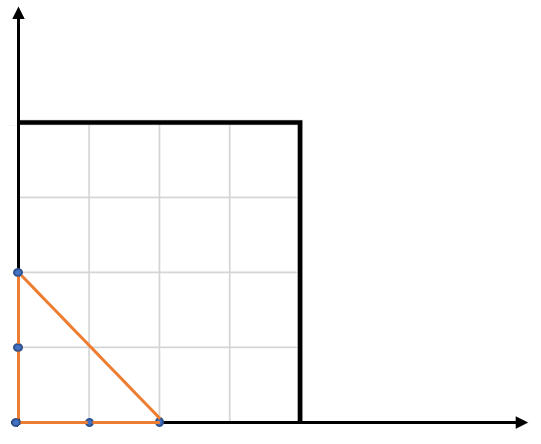
输入:points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出:2.00000
解释:输入中的 5 个点如上图所示,红色的三角形面积最大。示例 2:
输入:points = [[1,0],[0,0],[0,1]]
输出:0.50000提示:
- 3 <= points.length <= 50
- -50 <= xi, yi <= 50
- 给出的所有点 互不相同
思路
暴力解,三层循环,三角形面积可以使用向量的叉积计算。
向量的叉积表示这两个向量构成的平行四边形面积,除以 2 就是三角形的面积。
向量 (x1, y1) 与 (x2, y2) 的叉积等于 |x1 * y2 - x2 * y1|。
代码
/**
* @date 2025-09-27 21:35
*/
public class LargestTriangleArea812 {
public double largestTriangleArea(int[][] points) {
int n = points.length;
double res = 0.0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
for (int k = j + 1; k < n; k++) {
int p1 = points[i][0];
int q1 = points[i][1];
int p2 = points[j][0];
int q2 = points[j][1];
int p3 = points[k][0];
int q3 = points[k][1];
res = Math.max(res, Math.abs((p2 - p1) * (q3 - q1) - (p3 - p1) * (q2 - q1)));
}
}
}
return res / 2;
}
}
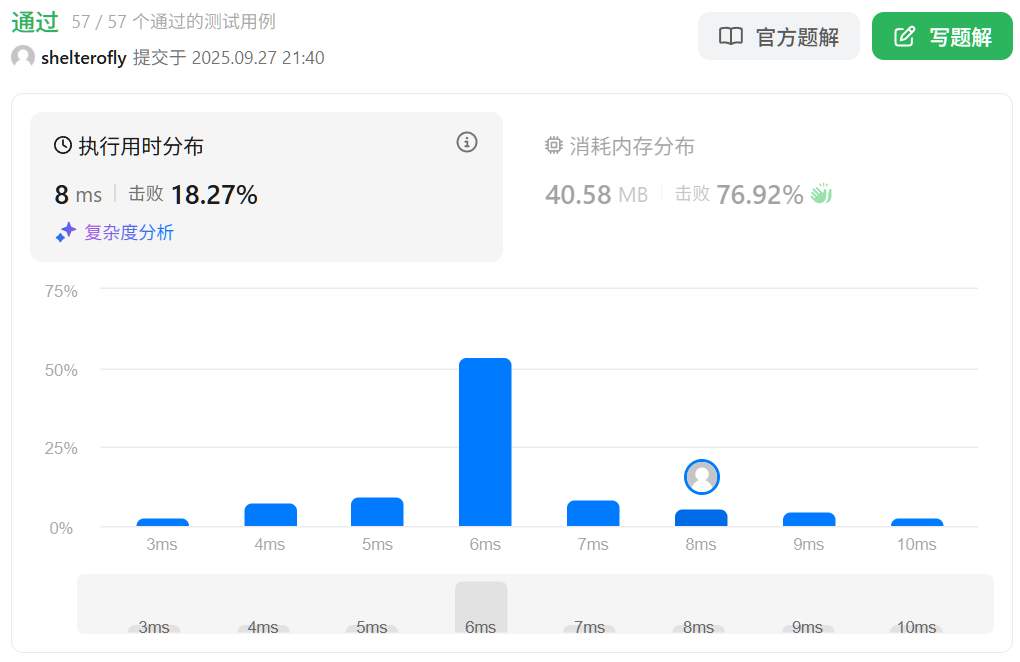
性能